Метод функций Ляпунова

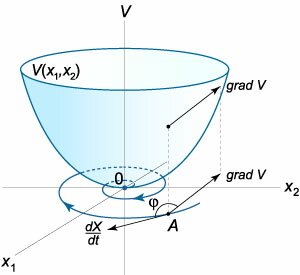
Функция Ляпунова представляет собой скалярную функцию, заданную на фазовом пространстве системы, с помощью которой можно доказать устойчивость положения равновесия. Метод функций Ляпунова применяется для исследования устойчивости различных дифференциальных уравнений и систем. Ниже мы ограничимся рассмотрением автономных систем \[ {\mathbf{X'} = \mathbf{f}\left( \mathbf{X} \right)\;\;\text{или}}\;\; {\frac{{d{x_i}}}{{dt}} = {f_i}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right),}\;\; {i = 1,2, \ldots ,n,} \] имеющих нулевое положение равновесия \(\mathbf{X} \equiv \mathbf{0}.\)

Предположим, что в некоторой окрестности \(U\) начала координат задана непрерывно дифференцируемая функция \[V\left( \mathbf{X} \right) = V\left( {{x_1},{x_2}, \ldots ,{x_n}} \right).\] Пусть \(V\left( \mathbf{X} \right) > 0\) для всех \(\mathbf{X} \in U\backslash \left\{ \mathbf{0} \right\},\) а в начале координат \(V\left( \mathbf{0} \right) = 0.\) Такими функциями являются, например, функции вида \[ {V\left( {{x_1},{x_2}} \right) = ax_1^2 + bx_2^2,}\;\; {V\left( {{x_1},{x_2}} \right) = ax_1^2 + bx_2^4,}\;\; {a,b > 0.} \] Найдем полную производную функции \(V\left( \mathbf{X} \right)\) по времени \(t:\) \[ {\frac{{dV}}{{dt}} = \frac{{\partial V}}{{\partial {x_1}}}\frac{{d{x_1}}}{{dt}} + \frac{{\partial V}}{{\partial {x_2}}}\frac{{d{x_2}}}{{dt}} + \cdots } + {\frac{{\partial V}}{{\partial {x_n}}}\frac{{d{x_n}}}{{dt}}.} \] Это выражение можно записать в виде скалярного произведения двух векторов: \[ {\frac{{dV}}{{dt}} = \left( {\text{grad}\,V,\frac{{d\mathbf{X}}}{{dt}}} \right),\;\;\text{где}\;\;} {V = \left( {\frac{{\partial V}}{{\partial {x_1}}},\frac{{\partial V}}{{\partial {x_2}}}, \ldots ,\frac{{\partial V}}{{\partial {x_n}}}} \right),}\;\; {\frac{{d\mathbf{X}}}{{dt}} = \left( {\frac{{d{x_1}}}{{dt}},\frac{{d{x_2}}}{{dt}}, \ldots ,\frac{{d{x_n}}}{{dt}}} \right).} \] Здесь первый вектор представляет собой градиент функции \(V\left( \mathbf{X} \right),\) т.е. он всегда направлен в сторону наибольшего возрастания функции \(V\left( \mathbf{X} \right).\) Как правило, функция \(V\left( \mathbf{X} \right)\) возрастает при удалении от начала координат, т.е. при условии \(\left| \mathbf{X} \right| \to \infty .\) Второй вектор в скалярном произведении − это вектор скорости движения. В любой точке он направлен по касательной к фазовой траектории.

Рассмотрим случай, когда производная функции \(V\left( \mathbf{X} \right)\) в окрестности \(U\) начала координат отрицательна: \[\frac{{dV}}{{dt}} = \left( {\text{grad}\,V,\frac{{d\mathbf{X}}}{{dt}}} \right) < 0.\] Это означает, что угол \(\varphi\) между вектором градиента и вектором скорости больше \(90^\circ.\) Для функции двух переменных это схематически показано на рисунках \(1\) и \(2.\) Очевидно, что если производная \(\large\frac{{dV}}{{dt}}\normalsize\) вдоль фазовой траектории всюду отрицательная, то траектория движения стремится к началу координат, т.е. система является устойчивой. В противном случае, когда производная \(\large\frac{{dV}}{{dt}}\normalsize\) положительна, траектория стремится от начала координат, т.е. система является неустойчивой.

Перейдем к строгим формулировкам.

Функция \(V\left( \mathbf{X} \right),\) непрерывно дифференцируемая в некоторой окрестности \(U\) начала координат, называется функцией Ляпунова автономной системы \[\mathbf{X'} = \mathbf{f}\left( \mathbf{X} \right),\] если выполнены следующие условия:

1. \(V\left( \mathbf{X} \right) > 0\) для всех \(\mathbf{X} \in U\backslash \left\{ \mathbf{0} \right\}\);

2. \(V\left( \mathbf{0} \right) = 0\);

3. \({\large\frac{{dV}}{{dt}}\normalsize} \le 0\) для всех \(\mathbf{X} \in U\).

Теорема об устойчивости в смысле Ляпунова. Если в некоторой окрестности \(U\) нулевого решения \(\mathbf{X} = \mathbf{0}\) автономной системы существует функция Ляпунова \(V\left( \mathbf{X} \right),\) то положение равновесия \(\mathbf{X} = \mathbf{0}\) является устойчивым по Ляпунову.

Теорема об асимптотической устойчивости. Если в некоторой окрестности \(U\) нулевого решения \(\mathbf{X} = \mathbf{0}\) автономной системы существует функция Ляпунова \(V\left( \mathbf{X} \right)\) с отрицательно определенной производной \({\large\frac{{dV}}{{dt}}\normalsize} < 0\) для всех \(\mathbf{X} \in U\backslash \left\{ \mathbf{0} \right\},\) то положение равновесия \(\mathbf{X} = \mathbf{0}\) является асимптотически устойчивым.

Как видно, для асимптотической устойчивости нулевого решения требуется, чтобы полная производная \({\large\frac{{dV}}{{dt}}\normalsize}\) была строго отрицательной (отрицательно определенной) в окрестности начала координат. Теорема Ляпунова о неустойчивости. Пусть в окрестности \(U\) нулевого решения \(\mathbf{X} = \mathbf{0}\) существует непрерывно дифференцируемая функция \(V\left( \mathbf{X} \right),\) такая, что

1. \(V\left( \mathbf{0} \right) = 0\);

2. \({\large\frac{{dV}}{{dt}}\normalsize} > 0\).

Если в окрестности \(U\) имеются точки, в которых \(V\left( \mathbf{X} \right) > 0,\) то нулевое решение \(\mathbf{X} = \mathbf{0}\) является неустойчивым.

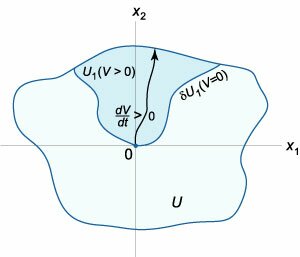
Теорема Четаева о неустойчивости. Пусть в окрестности \(U\) нулевого решения \(\mathbf{X} = \mathbf{0}\) автономной системы существует непрерывно дифференцируемая функция \(V\left( \mathbf{X} \right).\) Пусть окрестность \(U\) содержит подобласть \({U_1},\) включающую начало координат (рис.\(3\)), такую, что

1. \(V\left( \mathbf{X} \right) > 0\) для всех \(\mathbf{X} \in {U_1}\backslash \left\{ \mathbf{0} \right\}\);

2. \({\large\frac{{dV}}{{dt}}\normalsize} > 0\) для всех \(\mathbf{X} \in {U_1}\backslash \left\{ \mathbf{0} \right\}\);

3. \(V\left( \mathbf{X} \right) = 0\) для всех \(\mathbf{X} \in \delta {U_1},\) где \(\delta {U_1}\) обозначает границу подобласти \({U_1}\).

Тогда нулевое решение \(\mathbf{X} = \mathbf{0}\) системы неустойчиво. В этом случае фазовые траектории в подобласти \({U_1}\) будут стремиться от начала координат.

Таким образом, функции Ляпунова позволяют установить устойчивость или неустойчивость системы. Преимуществом данного метода является то, что здесь не требуется знать само решение \(\mathbf{X}\left( t \right).\) Кроме того, данный метод позволяет исследовать устойчивость положений равновесия негрубых систем, − например, в случае, когда точка равновесия является центром. Недостаток заключается в том, что не существует общего метода построения функций Ляпунова. В частном случае однородных автономных систем с постоянными коэффициентами функцию Ляпунова можно искать в виде квадратичной формы.

   Пример 1

Исследовать на устойчивость нулевое решение системы \[\frac{{dx}}{{dt}} = - 2x,\;\;\frac{{dy}}{{dt}} = x - y.\] Данная система представляет собой линейную однородную систему с постоянными коэффициентами. В качестве функции Ляпунова возьмем квадратичную форму \[V\left( \mathbf{X} \right) = V\left( {x,y} \right) = a{x^2} + b{y^2},\] где коэффициенты \(a, b\) подлежат определению.

Очевидно, что функция \(V\left( {x,y} \right)\) всюду положительна, кроме начала координат, где она равна нулю. Вычислим полную производную функции \(V\left( {x,y} \right):\) \[ {\frac{{dV}}{{dt}} = \frac{{\partial V}}{{\partial x}}\frac{{dx}}{{dt}} + \frac{{\partial V}}{{\partial y}}\frac{{dy}}{{dt}} } = {2ax\left( { - 2x} \right) + 2by\left( {x - y} \right) } = { - 4a{x^2} + 2bxy - 2b{y^2} } = { - 2b\left( {\frac{{4a}}{{2b}}{x^2} - xy + {y^2}} \right) } = { - 2b\left( {\frac{{2a}}{b}{x^2} - xy + {y^2}} \right).} \] Выражение в скобках можно преобразовать в квадрат разности, если выполняется условие \[\frac{{2a}}{b} = \frac{1}{4}\;\;\text{или}\;\;8a = b.\] Мы можем взять любую подходящую комбинацию, например, положим \(a = 1,\) \(b = 8.\) Тогда производная принимает вид: \[ {\frac{{dV}}{{dt}} = - 16\left( {\frac{{{x^2}}}{4} - xy + {y^2}} \right) } = { - 16{\left( {\frac{x}{2} - y} \right)^2} < 0.} \] Таким образом, для данной системы существует функция Ляпунова, причем ее производная всюду отрицательна за исключением начала координат. Следовательно, нулевое решение системы асимптотически устойчиво (устойчивый узел).

   Пример 2

Исследовать на устойчивость нулевое решение системы \[\frac{{dx}}{{dt}} = y,\;\;\frac{{dy}}{{dt}} = - x.\] Заметим, что для данной системы метод первого приближения неприменим, поскольку нулевое решение представляет собой "центр" (т.е. система не является грубой): \[ {A = \left( {\begin{array}{*{20}{r}} 0&1\\ { - 1}&0 \end{array}} \right),}\;\; {\det \left( {A - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} { - \lambda }&1\\ { - 1}&{ - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow {\lambda ^2} + 1 = 0,}\;\; {\Rightarrow {\lambda _{1,2}} = \pm i.} \] Воспользуемся методом функций Ляпунова для анализа устойчивости. Пусть функция \(V\left( \mathbf{X} \right)\) имеет вид \[V\left( \mathbf{X} \right) = V\left( {x,y} \right) = {x^2} + {y^2}.\] Вычислим производную функции \(V\left( \mathbf{X} \right)\) в силу данной системы: \[ {\frac{{dV}}{{dt}} = \frac{{\partial V}}{{\partial x}}\frac{{dx}}{{dt}} + \frac{{\partial V}}{{\partial y}}\frac{{dy}}{{dt}} } = {2x \cdot y + 2y \cdot \left( { - x} \right) \equiv 0.} \] Таким образом, производная тождественно равна нулю. Следовательно, функция \(V\left( \mathbf{X} \right)\) является функцией Ляпунова и нулевое решение системы устойчиво в смысле Ляпунова. Условие асимптотической устойчивости здесь не выполняется (для этого производная \({\large\frac{{dV}}{{dt}}\normalsize}\) должна быть отрицательной).

   Пример 3

Исследовать на устойчивость нулевое решение нелинейной системы \[\frac{{dx}}{{dt}} = - x{y^2},\;\;\frac{{dy}}{{dt}} = 3y{x^2}.\] Очевидно, что якобиан данной системы в точке \(\left( {0,0} \right)\) представляет собой нулевую матрицу: \[\require{AMSmath.js} J = {\left. {\left( {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}}}{{\partial x}}}&{\frac{{\partial {f_1}}}{{\partial y}}}\\ {\frac{{\partial {f_2}}}{{\partial x}}}&{\frac{{\partial {f_2}}}{{\partial y}}} \end{array}} \right)} \right|_{\substack{ x = 0\\ y = 0}}} = \left( {\begin{array}{*{20}{c}} 0&0\\ 0&0 \end{array}} \right).\] Собственные значения этой матрицы равны нулю: \({\lambda _{1,2}} = 0.\) Поэтому метод исследования устойчивости по первому приближению неприменим.

Посмотрим какой результат можно получить, используя функцию Ляпунова. В качестве такой функции возьмем \[V\left( \mathbf{X} \right) = V\left( {x,y} \right) = 3{x^2} + {y^2},\] которая является положительно определенной всюду, кроме начала координат. Вычислим полную производную: \[ {\frac{{dV}}{{dt}} = \frac{{\partial V}}{{\partial x}}\frac{{dx}}{{dt}} + \frac{{\partial V}}{{\partial y}}\frac{{dy}}{{dt}} } = {6x\left( { - x{y^2}} \right) + 2y\left( {3y{x^2}} \right) } = { - 6{x^2}{y^2} + 6{x^2}{y^2} \equiv 0.} \] Здесь снова, как и в предыдущем примере, производная тождественно равна нулю. Это значит, что нулевое решение системы устойчиво (в смысле Ляпунова).

   Пример 4

Исследовать на устойчивость нулевое решение системы, используя метод функций Ляпунова: \[\frac{{dx}}{{dt}} = y - 2x,\;\;\frac{{dy}}{{dt}} = 2x - y - {x^3}.\] В качестве возможной функции Ляпунова выберем функцию вида \[V\left( \mathbf{X} \right) = V\left( {x,y} \right) = {\left( {x + y} \right)^2} + \frac{{{x^4}}}{2}.\] Очевидно, эта функция является положительно определенной всюду, кроме начала координат, где она равна нулю. Вычислим ее производную (в силу данной системы): \[\require{cancel} {\frac{{dV}}{{dt}} = \frac{{\partial V}}{{\partial x}}\frac{{dx}}{{dt}} + \frac{{\partial V}}{{\partial y}}\frac{{dy}}{{dt}} } = {\left( {2x + 2y + 2{x^3}} \right)\left( {y - 2x} \right) + \left( {2x + 2y} \right)\left( {2x - y - {x^3}} \right) } = {\cancel{\left( {2x + 2y} \right)\left( {y - 2x} \right)} + 2{x^3}\left( {y - 2x} \right) } - {\cancel{\left( {2x + 2y} \right)\left( {y - 2x} \right)} - {x^3}\left( {2x + 2y} \right) } = {\cancel{2{x^3}y} - 4{x^4} - 2{x^4} - \cancel{2{x^3}y} = - 6{x^4} \le 0.} \] Как видно, производная является отрицательно определенной всюду, кроме точки \(\left( {0,0} \right).\) Тогда нулевое решение будет асимптотически устойчивым.

Используя метод первого приближения, можно убедиться, что нулевое положение равновесия представляет собой устойчивый фокус. Действительно, собственные значения линеаризованной системы являются комплексно-сопряженными числами с отрицательной действительной частью: \[ {J = \left( {\begin{array}{*{20}{r}} 1&{ - 2}\\ 2&{ - 1} \end{array}} \right),}\;\; {\det \left( {J - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} {1 - \lambda }&{ - 2}\\ 2&{ - 1 - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow {\left( {\lambda + 1} \right)^2} + 4 = 0,}\;\; {\Rightarrow {\left( {\lambda + 1} \right)^2} = - 4,}\;\; {\Rightarrow \left| {\lambda + 1} \right| = \pm 2i,}\;\; {\Rightarrow {\lambda _{1,2}} = - 1 \pm 2i.} \]

   Пример 5

Используя функцию Ляпунова, исследовать на устойчивость нулевое решение системы \[\frac{{dx}}{{dt}} = x + 3y,\;\;\frac{{dy}}{{dt}} = 2x.\] Возьмем в качестве функции \(V\left( \mathbf{X} \right)\) следующую функцию: \[V\left( \mathbf{X} \right) = V\left( {x,y} \right) = 2{x^2} - 3{y^2}.\] Выбор коэффициентов будет ясен из последующих преобразований. Вычислим полную производную функции \(V\left( \mathbf{X} \right)\) в силу данной системы: \[ {\frac{{dV}}{{dt}} = \frac{{\partial V}}{{\partial x}}\frac{{dx}}{{dt}} + \frac{{\partial V}}{{\partial y}}\frac{{dy}}{{dt}} } = {4x\left( {x + 3y} \right) - 6y\left( {2x} \right) } = {4{x^2} + \cancel{12xy} - \cancel{12xy} = 4{x^2} > 0.} \] Таким образом, производная \({\large\frac{{dV}}{{dt}}\normalsize}\) является положительно определенной всюду, кроме начала координат.

С другой стороны, можно найти точки, сколь угодно близкие к нулю, в которых функция \(V\left( \mathbf{X} \right)\) также будет положительной. Такие точки, например, расположены на оси \(Ox\) при \(y = 0.\)

Как видно, выполнены условия теоремы Ляпунова о неустойчивости. Следовательно, нулевое решение системы неустойчиво.

   Пример 6

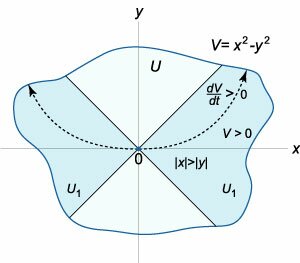
Исследовать на устойчивость нулевое решение системы \[\frac{{dx}}{{dt}} = {x^3} + y,\;\;\frac{{dy}}{{dt}} = x + {y^3}.\] Исходя из вида правых частей уравнений, можно заметить, что производные \({\large\frac{{dx}}{{dt}}\normalsize},\) \({\large\frac{{dy}}{{dt}}\normalsize}\) будут возрастать для точек в первом квадранте плоскости \(Oxy\) (при \(x > 0,\) \(y > 0\)). Поэтому можно предположить, что система является неустойчивой. Для доказательства воспользуемся теоремой Четаева.

Пусть функция \(V\left( \mathbf{X} \right)\) имеет вид \[V\left( \mathbf{X} \right) = V\left( {x,y} \right) = {x^2} - {y^2}.\] Эта функция является положительно определенной в подобласти \({U_1},\) в которой выполняется неравенство \(\left| x \right| > \left| y \right|\) (см. выше рис.\(4\)). Вычислим производную \({\large\frac{{dV}}{{dt}}\normalsize}\) в силу данной системы и определим ее знак в подобласти \({U_1}.\) \[ {\frac{{dV}}{{dt}} = \frac{{\partial V}}{{\partial x}}\frac{{dx}}{{dt}} + \frac{{\partial V}}{{\partial y}}\frac{{dy}}{{dt}} } = {2x\left( {{x^3} + y} \right) - 2y\left( {x + {y^3}} \right) } = {2{x^4} + \cancel{2xy} - \cancel{2xy} - 2{y^4} } = {2\left( {{x^4} - {y^4}} \right).} \] Видно, что производная \({\large\frac{{dV}}{{dt}}\normalsize}\) также является положительно определенной в подобласти \({U_1},\) определяемой соотношением \(\left| x \right| > \left| y \right|.\) Кроме того, функция \(V\left( \mathbf{X} \right)\) равна нулю на границе области \({U_1},\) включая точку \(\left( {0,0} \right).\) Таким образом, выполняются все условия теоремы Четаева. Следовательно, нулевое решение системы неустойчиво.

Вычислив собственные значения якобиана линеаризованной системы, можно убедиться, что нулевое положение равновесия является седлом: \[ {J = {\left. {\left( {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}}}{{\partial x}}}&{\frac{{\partial {f_1}}}{{\partial y}}}\\ {\frac{{\partial {f_2}}}{{\partial x}}}&{\frac{{\partial {f_2}}}{{\partial y}}} \end{array}} \right)} \right|_{\substack{ x = 0\\ y = 0}}} } = {{\left. {\left( {\begin{array}{*{20}{c}} {3{x^2}}&1\\ 1&{3{y^2}} \end{array}} \right)} \right|_{\substack{ x = 0\\ y = 0}}} } = {\left( {\begin{array}{*{20}{c}} 0&1\\ 1&0 \end{array}} \right);} \] \[ {\det \left( {J - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} { - \lambda }&1\\ 1&{ - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow {\lambda ^2} - 1 = 0,}\;\; {\Rightarrow {\lambda ^2} = 1,}\;\; {\Rightarrow {\lambda _{1,2}} = \pm 1.} \]