Критерий Рауса-Гурвица

Рассмотрим однородную систему дифференциальных уравнений \(n\)-го порядка с постоянными коэффициентами: \[ {\mathbf{X'}\left( t \right) = A\mathbf{X}\left( t \right),}\;\; {\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{x_2}\left( t \right)}\\ \vdots \\ {{x_n}\left( t \right)} \end{array}} \right),}\;\; {A = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \vdots &{{a_{1n}}}\\ {{a_{21}}}&{{a_{22}}}& \vdots &{{a_{2n}}}\\ \cdots & \cdots & \cdots & \cdots \\ {{a_{n1}}}&{{a_{n2}}}& \vdots &{{a_{nn}}} \end{array}} \right),} \] где \(\mathbf{X}\left( t \right)\) − \(n\)-мерный вектор, \(A\) − квадратная матрица размера \(n \times n.\)

Нелинейную автономную систему можно также свести к такой системе, выполнив линеаризацию вблизи точки равновесия. Далее без потери общности будем считать, что точка равновесия находится в начале координат. Этого всегда можно достигнуть выбором подходящей системы координат.

Устойчивость или неустойчивость положения равновесия определяется знаками действительных частей собственных значений матрицы \(A.\) Чтобы найти собственные значения \(\lambda,\) необходимо решить характеристическое уравнение \[\det \left( {A - \lambda I} \right) = 0,\] которое сводится к алгебраическому уравнению \(n\)-ой степени \[{a_0}{\lambda ^n} + {a_1}{\lambda ^{n - 1}} + {a_2}{\lambda ^{n - 2}} + \cdots + {a_{n - 1}}\lambda + {a_n} = 0.\] Корни такого уравнения легко вычисляются в случае \(n = 2\) и в некоторых случаях при \(n \ge 3.\) В остальных случаях решение характеристического уравнения представляет значительные трудности. Более того, Н.Х.Абелем (\(1802-1829\)) была доказана теорема, согласно которой при \(n \ge 5\) общее алгебраическое уравнение неразрешимо в радикалах, т.е. в общем случае не существует формул, выражающих корни уравнения через его коэффициенты в случае \(n \ge 5.\)

В такой ситуации большое значение имеют методы, позволяющие, не решая само характеристическое уравнение, определить, будут ли все его корни иметь отрицательную действительную часть, т.е. установить устойчивость системы. Одним из таких методов является критерий Рауса-Гурвица, который содержит необходимые и достаточные условия устойчивости системы.

Рассмотрим снова характеристическое уравнение \[{a_0}{\lambda ^n} + {a_1}{\lambda ^{n - 1}} + {a_2}{\lambda ^{n - 2}} + \cdots + {a_{n - 1}}\lambda + {a_n} = 0,\] описывающее динамическую систему. Заметим, что необходимое условие устойчивости выполняется, если все коэффициенты уравнения \({a_i} > 0.\) Поэтому далее считаем, что коэффициент \({a_0} > 0.\) Запишем так называемую матрицу Гурвица. Она составляется следующим образом. Главная диагональ матрицы содержит элементы \({a_1},{a_2}, \ldots ,{a_n}.\) Первый столбец содержит числа с нечетными индексами \({a_1},{a_3},{a_5}, \ldots \) В каждой строке индекс каждого следующего числа (считая слева направо) меньше на \(1\) индекса предыдущего числа. Все остальные коэффициенты \({a_i}\) с индексами больше \(n\) или меньше \(0\) заменяются нулями. В результате получаем матрицу, вида \[\left( {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}&0&0&0&0& \vdots &0\\ {{a_3}}&{{a_2}}&{{a_1}}&{{a_0}}&0&0& \vdots &0\\ {{a_5}}&{{a_4}}&{{a_3}}&{{a_2}}&{{a_1}}&{{a_0}}& \vdots &0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0&0&0&0&0&0& \vdots &{{a_n}} \end{array}} \right).\] Главные диагональные миноры \({\Delta _i}\) матрицы Гурвица определяются формулами \[ {{\Delta _1} = {a_1},\;\;{\Delta _2} = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}\\ {{a_3}}&{{a_2}} \end{array}} \right|,}\;\; {{\Delta _3} = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}&0\\ {{a_3}}&{{a_2}}&{{a_1}}\\ {{a_5}}&{{a_4}}&{{a_3}} \end{array}} \right|,}\;\; {{\Delta _n} = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}&0& \vdots &0\\ {{a_3}}&{{a_2}}&{{a_1}}& \vdots &0\\ {{a_5}}&{{a_4}}&{{a_3}}& \vdots &0\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 0&0&0& \vdots &{{a_n}} \end{array}} \right|.} \] Сформулируем теперь критерий устойчивости Рауса-Гурвица : Для того, чтобы все корни характеристического уравнения имели отрицательные действительные части, необходимо и достаточно, чтобы все главные диагональные миноры матрицы Гурвица были положительны при условии \({a_0} > 0:\) \({\Delta _1} > 0,\) \({\Delta _2} > 0,\ldots,\) \({\Delta _n} > 0.\) Поскольку \({\Delta _n} = {a_n}{\Delta _{n - 1}},\) то последнее неравенство можно записать как \({a_n} > 0.\)

Для наиболее распространенных систем \(2\)-го, \(3\)-го и \(4\)-го порядков получаем следующие критерии устойчивости:

Для системы \(2\)-го порядка условие устойчивости выглядит так: \[ {{a_0} > 0,\;\;{\Delta _1} = {a_1} > 0,}\;\; {{\Delta _2} = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}\\ {{a_3}}&{{a_2}} \end{array}} \right| = {a_1}{a_2} > 0} \] или \[{a_0} > 0,\;\;{a_1} > 0,\;\;{a_2} > 0,\] то есть все коэффициенты в квадратном характеристическом уравнении должны быть положительными. Другими словами, для системы \(2\)-го порядка необходимое условие устойчивости является одновременно и достаточным. Подчеркнем, что речь идет об асимптотической устойчивости нулевого решения.

Для системы \(3\)-го порядка критерий устойчивости определяется неравенствами \[ {{a_0} > 0,\;\;{\Delta _1} = {a_1} > 0,}\;\; {{\Delta _2} = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}\\ {{a_3}}&{{a_2}} \end{array}} \right| } = {{a_1}{a_2} - {a_0}{a_3} > 0,}\;\; {{\Delta _3} = {a_3} > 0.} \] или \[ {{a_0} > 0,\;\;{a_1} > 0,}\;\; {{a_2} > 0,}\;\; {{a_3} > 0,}\;\; {{a_1}{a_2} - {a_0}{a_3} > 0.} \] Аналогично, для системы \(4\)-го порядка получаем следующую совокупность неравенств: \[ {{a_0} > 0,\;\;{\Delta _1} = {a_1} > 0,}\;\; {{\Delta _2} = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}\\ {{a_3}}&{{a_2}} \end{array}} \right| = {a_1}{a_2} - {a_0}{a_3} > 0,}\;\; {{\Delta _3} = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}&0\\ {{a_3}}&{{a_2}}&{{a_1}}\\ 0&{{a_4}}&{{a_3}} \end{array}} \right| } = {{a_1}{a_2}{a_3} - a_1^2{a_4} - {a_0}a_3^2 > 0,}\;\; {{\Delta _4} = {a_4} > 0} \] или \[ {{a_i} > 0\;\left( {i = 0, \ldots ,4} \right),}\;\;\; {{a_1}{a_2} - {a_0}{a_3} > 0,}\;\;\; {{a_1}{a_2}{a_3} - a_1^2{a_4} - {a_0}a_3^2 > 0.} \] Если все \(n - 1\) главных миноров Гурвица положительны, а минор \(n\)-го порядка равен нулю: \({\Delta _n} = 0,\) то система находится на границе устойчивости. Так как \({\Delta _n} = {a_n}{\Delta _{n - 1}},\) то возможны два случая:

1. Коэффициент \({a_n} = 0.\) Это соответствует случаю, когда один из корней характеристического уравнения равен нулю. Система находится на границе апериодической устойчивости.

2. Определитель \({\Delta _{n - 1}} = 0.\) В этом случае существуют два комплексно-сопряженных мнимых корня. Система находится на границе колебательной устойчивости.

Критерий устойчивости Рауса-Гурвица относится к семейству алгебраических критериев. Его удобно применять для анализа устойчивости систем низкого порядка. С увеличением порядка сложность вычислений заметно возрастает. В таких случаях может оказаться предпочтительным использование других критериев, например, теоремы Льенара-Шипара или частотного критерия Найквиста-Михайлова.

   Пример 1

Исследовать устойчивость нулевого решения уравнения \[x''' + 6x'' + 3x' + 2x = 0.\] Запишем характеристическое уравнение: \[{\lambda ^3} + 6{\lambda ^2} + 3\lambda + 2 = 0.\] Здесь коэффициенты \({a_i}\) равны \[ {{a_0} = 1,\;\;{a_1} = 6,}\;\; {{a_2} = 3,\;\;{a_3} = 2.} \] Составим матрицу Гурвица \[\left( {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}&0\\ {{a_3}}&{{a_2}}&{{a_1}}\\ 0&{{a_4}}&{{a_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 6&1&0\\ 2&3&6\\ 0&0&2 \end{array}} \right)\] и вычислим ее главные миноры: \[ {{\Delta _1} = 6 > 0,}\;\; {{\Delta _2} = \left| {\begin{array}{*{20}{c}} 6&1\\ 2&3 \end{array}} \right| = 18 - 2 = 16 > 0,}\;\; {{\Delta _3} = {a_3}{\Delta _2} = 2 \cdot 16 = 32 > 0.} \] Как видно, все миноры положительны. Следовательно, нулевое решение данного уравнения асимптотически устойчиво.

   Пример 2

Исследовать на устойчивость нулевое решение дифференциального уравнения \[{x^{IV}} + 2x''' + 4x'' + 7x' + 3x = 0.\] Составим характеристическое уравнение: \[{\lambda ^4} + 2{\lambda ^3} + 4{\lambda ^2} + 7\lambda + 3 = 0.\] Коэффициенты \({a_i}\) в этом уравнении равны \[ {{a_0} = 1,\;\;{a_1} = 2,\;\;{a_2} = 4,}\;\; {{a_3} = 7,\;\;{a_4} = 3.} \] Запишем матрицу Гурвица и найдем ее главные диагональные миноры: \[\left( {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}&0&0\\ {{a_3}}&{{a_2}}&{{a_1}}&{{a_0}}\\ 0&{{a_4}}&{{a_3}}&{{a_2}}\\ 0&0&0&{{a_4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 2&1&0&0\\ 7&7&2&1\\ 0&3&7&4\\ 0&0&0&3 \end{array}} \right);\] \[ {{\Delta _1} = 2 > 0,}\;\; {{\Delta _2} = \left| {\begin{array}{*{20}{c}} 2&1\\ 7&4 \end{array}} \right| = 8 - 7 = 1 > 0,}\;\; {{\Delta _3} = \left| {\begin{array}{*{20}{c}} 2&1&0\\ 7&4&2\\ 0&3&7 \end{array}} \right| } = { - 2 \cdot \left| {\begin{array}{*{20}{c}} 2&1\\ 0&3 \end{array}} \right| + 7 \cdot \left| {\begin{array}{*{20}{c}} 2&1\\ 7&4 \end{array}} \right| } = { - 12 + 7 = - 5 < 0.} \] В ходе расчетов мы получили отрицательный минор \({\Delta _3} < 0.\) Это означает, что нулевое решение уравнения неустойчиво.

   Пример 3

При каких значениях параметров \(\alpha\) и \(\beta\) нулевое решение уравнения \[{x^{IV}} + x''' + \alpha x'' + \beta x' + x = 0\] является асимптотически устойчивым?

Характеристическое уравнение записывается в виде \[{\lambda ^4} + {\lambda ^3} + \alpha {\lambda ^2} + \beta \lambda + 1 = 0.\] Здесь коэффициенты имеют следующие значения: \[ {{a_0} = 1,\;\;{a_1} = 1,\;\;{a_2} = \alpha,}\;\; {{a_3} = \beta,\;\;{a_4} = 1.} \] Составим матрицу Гурвица \[\left( {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}&0&0\\ {{a_3}}&{{a_2}}&{{a_1}}&{{a_0}}\\ 0&{{a_4}}&{{a_3}}&{{a_2}}\\ 0&0&0&{{a_4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&1&0&0\\ \beta&\alpha&1&1\\ 0&1&\beta&\alpha\\ 0&0&0&1 \end{array}} \right)\] и запишем условие устойчивости Рауса-Гурвица: \[{\Delta _1} = 1 > 0,\] \[{\Delta _2} = \left| {\begin{array}{*{20}{c}} 1&1\\ \beta &\alpha \end{array}} \right| = \alpha - \beta > 0,\] \[ {{\Delta _3} = \left| {\begin{array}{*{20}{c}} 1&1&0\\ \beta &\alpha &1\\ 0&1&\beta \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} \alpha &1\\ 1&\beta \end{array}} \right| - \beta \left| {\begin{array}{*{20}{c}} 1&0\\ 0&\beta \end{array}} \right| } = {\alpha \beta - 1 - {\beta ^2} } = {\beta \left( {\alpha - \beta } \right) - 1 > 0,} \] \[{\Delta _4} = {a_4}{\Delta _3} > 0,\;\; \Rightarrow {a_4} = 1 > 0.\] Таким образом, система неравенств, описывающих область устойчивости, выглядит так: \[\left\{ \begin{array}{l} {\Delta _2} > 0\\ {\Delta _3} > 0 \end{array} \right.,\;\; \Rightarrow \left\{ {\begin{array}{*{20}{l}} {\alpha - \beta > 0}\\ {\beta \left( {\alpha - \beta } \right) > 1} \end{array}} \right..\] Рассмотрим сначала второе неравенство. Решим его относительно \(\alpha.\) Здесь возникают два случая:

1. Если \(\beta > 0,\) то разделив обе части неравенства на \(\beta,\) получаем: \[\alpha - \beta > \frac{1}{\beta },\;\; \Rightarrow \alpha > \beta + \frac{1}{\beta };\]

2. Если \(\beta < 0,\) то соответственно имеем: \[\alpha - \beta < \frac{1}{\beta },\;\; \Rightarrow \alpha < \beta + \frac{1}{\beta }.\]

Очевидно, что случай \(\beta = 0\) не удовлетворяет данному неравенству.

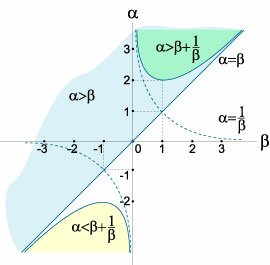
Итак, решением неравенства являются две бесконечные области, симметричные относительно начала координат и ограниченные кривой \(\alpha = \beta + \large\frac{1}{\beta }\normalsize\) (рис.\(1\)). Первому неравенству \(\alpha > \beta\) удовлетворяет множество точек выше прямой \(\alpha = \beta.\) В результате решением всей системы является лишь область \(\alpha > \beta + \large\frac{1}{\beta }\normalsize,\) расположенная в правом верхнем квадранте (при \(\beta > 0,\) \(\alpha > 0\)). На рисунке \(1\) эта область показана зеленым цветом. Данный участок на плоскости \(\left( {\beta ,\alpha } \right)\) представляет собой область асимптотической устойчивости исходного уравнения.

   Пример 4

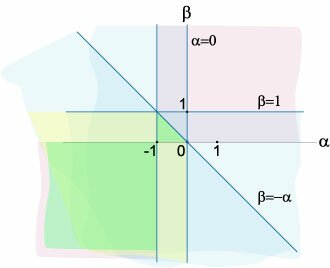
Исследовать, при каких значениях параметров \(\alpha\) и \(\beta\) нулевое решение системы является асимптотически устойчивым: \[ {\frac{{dx}}{{dt}} = \alpha x + \beta y,}\;\; {\frac{{dy}}{{dt}} = x - z,}\;\; {\frac{{dz}}{{dt}} = - x + y.} \] Составим характеристическое уравнение: \[ {\left| {\begin{array}{*{20}{c}} {\alpha - \lambda }&\beta &0\\ 1&{ - \lambda }&{ - 1}\\ { - 1}&1&{ - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \left( {\alpha - \lambda } \right)\left| {\begin{array}{*{20}{r}} { - \lambda }&{ - 1}\\ 1&{ - \lambda } \end{array}} \right| - \beta \left| {\begin{array}{*{20}{r}} 1&{ - 1}\\ { - 1}&{ - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \left( {\alpha - \lambda } \right)\left( {{\lambda ^2} + 1} \right) - \beta \left( { - \lambda - 1} \right) = 0,}\;\; {\Rightarrow \alpha {\lambda ^2} - {\lambda ^3} + \alpha - \lambda + \beta \lambda + \beta = 0,}\;\; {\Rightarrow {\lambda ^3} - \alpha {\lambda ^2} + \left( {1 - \beta } \right)\lambda - \alpha - \beta = 0.} \] Здесь коэффициенты \({a_i}\) имеют такие значения: \[ {{a_0} = 1,\;\;{a_1} = - \alpha ,}\;\; {{a_2} = 1 - \beta ,}\;\; {{a_3} = - \alpha - \beta .} \] Выясним сначала, при каких параметрах \(\alpha\) и \(\beta\) выполняется необходимое условие устойчивости: \[{a_i} > 0,\;\;i = 0,1,2,3.\] Получаем следующую систему неравенств: \[\left\{ \begin{array}{l} - \alpha > 0\\ 1 - \beta > 0\\ - \alpha - \beta > 0 \end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l} \alpha < 0\\ \beta < 1\\ \beta < - \alpha \end{array} \right..\] Решение этой системы удобно изобразить графически на плоскости \(\left( {\alpha ,\beta } \right).\) На рисунке \(2\) показаны прямые \(\alpha = 0,\) \(\beta = 1,\) \(\beta = -\alpha\) и области, соответствующие решениям каждого неравенства. Пересечение этих областей отмечено желтым цветом.

Теперь рассмотрим достаточные условия устойчивости. Запишем матрицу Гурвица: \[\left( {\begin{array}{*{20}{c}} {{a_1}}&{{a_0}}&0\\ {{a_3}}&{{a_2}}&{{a_1}}\\ 0&0&{{a_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - \alpha }&1&0\\ { - \alpha - \beta }&{1 - \beta }&{ - \alpha }\\ 0&0&{ - \alpha - \beta } \end{array}} \right).\] Главные диагональные миноры \({\Delta _i}\) имеют вид: \[{\Delta _1} = - \alpha ,\] \[\require{cancel} {{\Delta _2} = \left| {\begin{array}{*{20}{c}} { - \alpha }&1\\ { - \alpha - \beta }&{1 - \beta } \end{array}} \right| } = {\alpha \left( {\beta - 1} \right) + \alpha + \beta } = {\alpha \beta - \cancel{\alpha} + \cancel{\alpha} + \beta } = {\left( {\alpha + 1} \right)\beta ,} \] \[{\Delta _3} = {a_3}{\Delta _2} = \left( { - \alpha - \beta } \right)\left( {\alpha + 1} \right)\beta .\] Согласно критерию устойчивости Рауса-Гурвица должны соблюдаться следующие неравенства: \[ {{\Delta _1} = - \alpha > 0,}\;\;\; {{\Delta _2} = \left( {\alpha + 1} \right)\beta > 0,}\;\;\; {{a_3} > 0.} \] Из этих неравенств дополнительным (по сравнению с необходимыми условиями) является лишь неравенство \[\;{\Delta _2} > 0\;\;\;\text{или}\;\;\;\left( {\alpha + 1} \right)\beta > 0.\] Его решение содержит два случая:

1. \(\beta > 0,\;\; \Rightarrow \alpha + 1 > 0\;\;\text{или}\;\;\alpha > - 1;\)

2. \(\beta < 0,\;\; \Rightarrow \alpha + 1 < 0\;\;\text{или}\;\;\alpha < - 1.\)

Этим двум случаям соответствуют два квадранта, ограниченные прямыми \(\alpha = -1,\) \(\beta = 0\) (на рисунке 2 они изображаются фиолетовым цветом).

Область устойчивости системы ограничена значениями параметров \(\alpha, \beta,\) при которых выполняются как необходимые, так и достаточные условия асимптотической устойчивости. Эта область состоит из левого нижнего квадранта, ограниченного прямыми \(\alpha = -1,\) \(\beta = 0,\) и прямоугольного треугольника с вершинами \(\left( {0,0} \right),\) \(\left( {-1,0} \right),\) \(\left( {-1,1} \right).\) Окончательно область устойчивости отмечена на рисунке зеленым цветом.