Криволинейные интегралы первого рода

Пусть кривая \(C\) описывается векторной функцией \(\mathbf{r} = \mathbf{r}\left( s \right),\) \(0 \le s \le S,\) где переменная \(s\) представляет собой длину дуги кривой (рисунок \(1\)).

Если на кривой \(C\) определена скалярная функция \(F,\) то интеграл \(\int\limits_0^S {F\left( {\mathbf{r}\left( s \right)} \right)ds} \) называется криволинейным интегралом первого рода от скалярной функции \(F\) вдоль кривой \(C\) и обозначается как \[\int\limits_C {F\left( {x,y,z} \right)ds} \;\;\;\text{или}\;\;\int\limits_C {Fds} .\] Криволинейный интеграл \(\int\limits_C {Fds}\) существует, если функция \(F\) непрерывна на кривой \(C.\) Криволинейный интеграл \(I\) рода обладает следующими свойствами:

1. Интеграл не зависит от ориентации кривой;

2. Пусть кривая \({C_1}\) начинается в точке \(A\) и заканчивается в точке \(B,\) а кривая \({C_2}\) начинается в точке \(B\) и заканчивается в точке \(D\) (рисунок \(2\)). Тогда их объединением будет называться кривая \({C_1} \cup {C_2},\) которая проходит от \(A\) к \(B\) вдоль кривой \({C_1}\) и затем от \(B\) к \(D\) вдоль кривой \({C_2}.\) Для криволинейных интегралов первого рода справедливо соотношение \[\int\limits_{{C_1} \cup {C_2}} {Fds} = \int\limits_{{C_1}} {Fds} + \int\limits_{{C_2}} {Fds} ;\]

3. Если гладкая кривая \(C\) задана параметрически соотношением \(\mathbf{r} = \mathbf{r}\left( t \right),\) \(\alpha \le t \le \beta \) и скалярная функция \(F\) непрерывна на кривой \(C,\) то \[ {\int\limits_C {F\left( {x,y,z} \right)ds} } = {\int\limits_\alpha ^\beta {F\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\sqrt {{{\left( {x'\left( t \right)} \right)}^2} + {{\left( {y'\left( t \right)} \right)}^2} + {{\left( {z'\left( t \right)} \right)}^2}} dt} ;} \]

4. Если \(C\) является гладкой кривой в плоскости \(Oxy,\) заданной уравнением \(y = f\left( x \right),\) \(a \le x \le b,\) то \[ {\int\limits_C {F\left( {x,y} \right)ds} } = {\int\limits_a^b {F\left( {x,f\left( x \right)} \right)\sqrt {1 + {{\left( {f'\left( x \right)} \right)}^2}} dx} ;} \]

5. Если гладкая кривая \(C\) в плоскости \(Oxy\) определена уравнением \(x = \varphi \left( y \right),\) \(c \le y \le d,\) то \[ {\int\limits_C {F\left( {x,y} \right)ds} } = {\int\limits_c^d {F\left( {\varphi \left( y \right),y} \right)\sqrt {1 + {{\left( {\varphi '\left( y \right)} \right)}^2}} dy} ;} \]

6. В полярных координатах интеграл \(\int\limits_C {F\left( {x,y} \right)ds} \) выражается формулой \[ {\int\limits_C {F\left( {x,y} \right)ds} } = {\int\limits_\alpha ^\beta {F\left( {r\cos \theta ,r\sin \theta } \right)\sqrt {{r^2} + {{\left( {\frac{{dr}}{{d\theta }}} \right)}^2}} d\theta } ,} \] где кривая \(C\) задана в полярных координатах функцией \(r\left( \theta \right).\)

   Пример 1

Найти интеграл \(\int\limits_C {{x^2}yds} \) вдоль отрезка прямой \(y = x\) от начала координат до точки \(\left( {2,2} \right)\) (рисунок \(3\)). \[ {\int\limits_C {{x^2}yds} = \int\limits_0^2 {{x^2} \cdot x\sqrt {1 + {1^2}} dx} } = {\sqrt 2 \int\limits_0^2 {{x^3}dx} } = {\sqrt 2 \left[ {\left. {\left( {\frac{{{x^4}}}{4}} \right)} \right|_0^2} \right] } = {4\sqrt 2 .} \]

   Пример 2

Вычислить интеграл \(\int\limits_C {{y^2}ds},\) где \(C\) − дуга окружности \(x = a\cos t,\) \(y = a\sin t,\) \(0 \le t \le \large\frac{\pi }{2}\normalsize.\) Запишем дифференциал дуги кривой: \[ {ds = \sqrt {{{\left( {x'\left( t \right)} \right)}^2} + {{\left( {y'\left( t \right)} \right)}^2}} dt } = {\sqrt {{a^2}{{\sin }^2}t + {a^2}{{\cos }^2}t} dt = adt.} \] Тогда, применяя формулу \[ {\int\limits_C {F\left( {x,y,z} \right)ds} } = {\int\limits_\alpha ^\beta {F\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\sqrt {{{\left( {x'\left( t \right)} \right)}^2} + {{\left( {y'\left( t \right)} \right)}^2} + {{\left( {z'\left( t \right)} \right)}^2}} dt} } \] в плоскости \(Oxy,\) получаем \[ {\int\limits_C {{y^2}ds} = \int\limits_0^{\large\frac{\pi }{2}\normalsize} {{a^2}{{\sin }^2}t \cdot adt} } = {{a^3}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\sin }^2}tdt} } = {\frac{{{a^3}}}{2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {1 - \cos 2t} \right)dt} } = {\frac{{{a^3}}}{2}\left[ {\left. {\left( {t - \frac{{\sin 2t}}{2}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\frac{{{a^3}}}{2} \cdot \frac{\pi }{2} } = {\frac{{{a^3}\pi }}{4}.} \]

   Пример 3

Вычислить интеграл \(\int\limits_C {{x^2}ds},\) где \(C\) − кривая, заданная уравнением \(y = f\left( x \right) = \ln x,\) \(1 \le x \le e.\) Используем формулу \[ {\int\limits_C {F\left( {x,y} \right)ds} } = {\int\limits_a^b {F\left( {x,f\left( x \right)} \right)\sqrt {1 + {{\left( {f'\left( x \right)} \right)}^2}} dx}.} \] Здесь \[ {\sqrt {1 + {{\left( {f'\left( x \right)} \right)}^2}} } = {\sqrt {1 + {{\left[ {{{\left( {\ln x} \right)}^\prime }} \right]}^2}} } = {\sqrt {1 + \frac{1}{{{x^2}}}} } = {\frac{{\sqrt {1 + {x^2}} }}{x}.} \] Следовательно, \[ {\int\limits_C {{x^2}ds} = \int\limits_1^e {{x^2}\frac{{\sqrt {1 + {x^2}} }}{x}dx} } = {\int\limits_1^e {\sqrt {1 + {x^2}} xdx} } = {\frac{1}{2}\int\limits_1^e {\sqrt {1 + {x^2}} d\left( {1 + {x^2}} \right)} } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{{{\left( {1 + {x^2}} \right)}^{\large\frac{3}{2}\normalsize}}}}{{\frac{3}{2}}}} \right)} \right|_1^e} \right] } = {\frac{1}{3}\left[ {{{\left( {1 + {e^2}} \right)}^{\large\frac{3}{2}\normalsize}} - {2^{\large\frac{3}{2}\normalsize}}} \right] } = {\frac{{\sqrt {{{\left( {1 + {e^2}} \right)}^3}} - \sqrt 8 }}{3} \approx 7,16.} \]

   Пример 4

Вычислить интеграл \(\int\limits_C {ds},\) где \(C\) является отрезком прямой от точки \(O\left( {0,0} \right)\) до \(A\left( {1,2} \right)\) (рисунок \(4\) выше). Найдем сначала уравнение отрезка \(OA.\) \[ {\frac{{y - {y_O}}}{{{y_A} - {y_O}}} = \frac{{x - {x_O}}}{{{x_A} - {x_O}}},}\;\; {\Rightarrow \frac{{y - 0}}{{2 - 0}} = \frac{{x - 0}}{{1 - 0}},}\;\; {\Rightarrow \frac{y}{2} = \frac{x}{1}\;\;\text{или}\;\;y = 2x.} \] Применяя формулу \[ {\int\limits_C {F\left( {x,y} \right)ds} } = {\int\limits_a^b {F\left( {x,f\left( x \right)} \right)\sqrt {1 + {{\left( {f'\left( x \right)} \right)}^2}} dx},} \] находим искомый криволинейный интеграл. \[ {\int\limits_C {ds} = \int\limits_0^1 {\sqrt {1 + {2^2}} dx} } = {\sqrt 5 \int\limits_0^1 {dx} } = {\sqrt 5 \cdot \left[ {\left. x \right|_0^1} \right] = \sqrt 5 .} \]

   Пример 5

Вычислить интеграл \(\int\limits_C {\left( {{x^2} + {y^2}} \right)zds},\) где кривая \(C\) задана параметрически в виде \(\mathbf{r}\left( t \right) = \left( {\sin 3t,\cos 3t,4t} \right),\) \(0 \le t \le \pi .\) Применяя формулу \[ {\int\limits_C {F\left( {x,y,z} \right)ds} } = {\int\limits_\alpha ^\beta {F\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\sqrt {{{\left( {x'\left( t \right)} \right)}^2} + {{\left( {y'\left( t \right)} \right)}^2} + {{\left( {z'\left( t \right)} \right)}^2}} dt},} \] можно записать \[ {\int\limits_C {\left( {{x^2} + {y^2}} \right)zds} } = {\int\limits_0^\pi {\left( {{{\sin }^2}3t + {{\cos }^2}3t} \right) \cdot 4t \cdot \sqrt {{{\left( {3\cos 3t} \right)}^2} + {{\left( { - 3\sin 3t} \right)}^2} + 16} \,dt} } = {4\int\limits_0^\pi {t\sqrt {9\left( {{{\cos }^2}3t + {{\sin }^2}3t} \right) + 16} \,dt} } = {20\int\limits_0^\pi {tdt} } = {20\left[ {\left. {\left( {\frac{{{t^2}}}{2}} \right)} \right|_0^\pi } \right] } = {10{\pi ^2}.} \]

   Пример 6

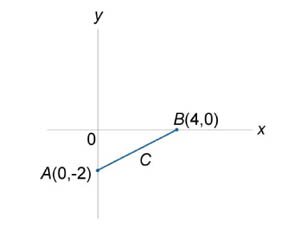
Вычислить криволинейный интеграл \(\int\limits_C {\large\frac{{ds}}{{y - x}}\normalsize},\) где кривая \(C\) − отрезок прямой от точки \(\left( {0, - 2} \right)\) до \(\left( {4, 0} \right)\) (рисунок \(5\)). Найдем уравнение отрезка \(AB.\) \[ {\frac{{y - {y_A}}}{{{y_B} - {y_A}}} = \frac{{x - {x_A}}}{{{x_B} - {x_A}}},}\;\; {\Rightarrow \frac{{y + 2}}{{0 + 2}} = \frac{{x - 0}}{{4 - 0}},}\;\; {\Rightarrow \frac{y + 2}{2} = \frac{x}{4}\;\;\text{или}\;\;y = \frac {x}{2} - 2.} \] По формуле \[ {\int\limits_C {F\left( {x,y} \right)ds} } = {\int\limits_a^b {F\left( {x,f\left( x \right)} \right)\sqrt {1 + {{\left( {f'\left( x \right)} \right)}^2}} dx}} \] находим заданный интеграл: \[ {\int\limits_C {\frac{{ds}}{{y - x}}} } = {\int\limits_0^4 {\frac{1}{{\frac{x}{2} - 2 - x}}\sqrt {1 + {{\left( {\frac{1}{2}} \right)}^2}} dx} } = {\int\limits_0^4 {\frac{1}{{ - 2 - \frac{x}{2}}}\sqrt {\frac{5}{4}} dx} } = { - \frac{{\sqrt 5 }}{2}\int\limits_0^4 {\frac{{dx}}{{x + 4}}} } = { - \sqrt 5 \left[ {\left. {\left( {\ln \left| {x + 4} \right|} \right)} \right|_0^4} \right] } = { - \sqrt 5 \left( {\ln 8 - \ln 4} \right) } = { - \sqrt 5 \ln 2 \approx - 1,55.} \]

   Пример 7

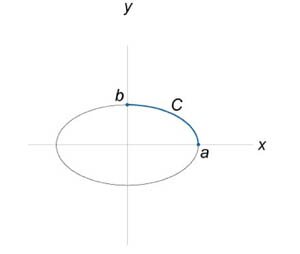
Найти криволинейный интеграл \(\int\limits_C {xyds},\) где кривая \(C\) является дугой эллипса \({\large\frac{{{x^2}}}{{{a^2}}}\normalsize} + {\large\frac{{{y^2}}}{{{b^2}}}\normalsize} = 1,\) лежащей в первом квадранте (рисунок \(6\)). Запишем уравнение эллипса в параметрической форме: \[ {\left\{ \begin{array}{l} x = a\cos t\\ y = b\sin t \end{array} \right.,}\;\; {0 \le t \le 2\pi .} \] Диапазон изменений \(t\) для первого квадранта равен \(0 \le t \le \large\frac{\pi }{2}\normalsize .\) Следовательно, по формуле \[ {\int\limits_C {F\left( {x,y} \right)ds} } = {\int\limits_\alpha ^\beta {F\left( {x\left( t \right),y\left( t \right)} \right)\sqrt {{{\left( {x'\left( t \right)} \right)}^2} + {{\left( {y'\left( t \right)} \right)}^2} } dt} } \] заданный интеграл преобразуется следующим образом: \[ {I = \int\limits_C {xyds} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {a\cos t \cdot b\sin t \cdot \sqrt {{{\left( { - a\sin t} \right)}^2} + {{\left( {b\cos t} \right)}^2}} dt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {a\cos t \cdot b\sin t \cdot \sqrt {{a^2}{{\sin }^2}t + {b^2}{\cos^2}t} dt} .} \] Сделаем замену переменной. Положим \(a\sin t = u\) или \(\sin t = \large\frac{u}{a}\normalsize .\) Тогда \[ {a\cos tdt = du,}\;\;\; {{b^2}{\cos ^2}t = {b^2}\left( {1 - {{\sin }^2}t} \right) } = {{b^2}\left[ {1 - {{\left( {\frac{u}{a}} \right)}^2}} \right].} \] Уточним пределы интегрирования. Если \(t = 0,\) то \(u = 0,\) а при \(t = \large\frac{\pi }{2}\normalsize\) получаем \(u = a.\) В результате интеграл становится равным \[ {I = \int\limits_0^a {u \cdot b \cdot \frac{{du}}{a} \cdot \sqrt {{u^2} + \frac{{{b^2}}}{{{a^2}}}\left( {{a^2} - {u^2}} \right)} du} } = {\frac{b}{a}\int\limits_0^a {\sqrt {{u^2} + {b^2} - \frac{{{b^2}}}{{{a^2}}}{u^2}} udu} } = {\frac{b}{a}\int\limits_0^a {\sqrt {{b^2} + \left( {1 - \frac{{{b^2}}}{{{a^2}}}} \right){u^2}} udu} .} \] Для вычисления полученного интеграла удобно сделать еще одну замену. \[ {p = {b^2} + \left( {1 - \frac{{{b^2}}}{{{a^2}}}} \right){u^2},}\;\; {\Rightarrow dp = \left( {1 - \frac{{{b^2}}}{{{a^2}}}} \right) \cdot 2udu,}\;\; {\Rightarrow udu = \frac{{{a^2}dp}}{{2\left( {{a^2} - {b^2}} \right)}}.} \] Если \(u = 0,\) то \(p = {b^2}\) и, соответственно, если \(u = a,\) то \(p = {a^2}.\) Таким образом, \[ {I = \frac{b}{a}\int\limits_{{b^2}}^{{a^2}} {\sqrt p \frac{{{a^2}}}{{2\left( {{a^2} - {b^2}} \right)}}dp} } = {\frac{{ab}}{{2\left( {{a^2} - {b^2}} \right)}}\int\limits_{{b^2}}^{{a^2}} {\sqrt p dp} } = {\frac{{ab}}{{2\left( {{a^2} - {b^2}} \right)}}\left[ {\left. {\left( {\frac{{{p^{\frac{3}{2}}}}}{{\frac{3}{2}}}} \right)} \right|_{{b^2}}^{{a^2}}} \right] } = {\frac{{ab}}{{2\left( {{a^2} - {b^2}} \right)}} \cdot \frac{2}{3}\left( {{a^3} - {b^3}} \right) } = {\frac{{ab}}{{3\left( {a - b} \right)}} \cdot \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) } = {\frac{{ab\left( {{a^2} + ab + {b^2}} \right)}}{{3\left( {a + b} \right)}}.} \]