Комплексная форма рядов Фурье

Пусть функция \(f\left( x \right)\) определена в интервале \(\left[ { - \pi ,\pi } \right].\) Применяя формулы Эйлера \[ {\cos \varphi = \frac{{{e^{i\varphi }} + {e^{ - i\varphi }}}}{2},}\;\; {\sin \varphi = \frac{{{e^{i\varphi }} - {e^{ - i\varphi }}}}{{2i}},} \] можно записать ряд Фурье данной функции в комплексной форме: \[ {f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos nx + {b_n}\sin nx} \right)} } = {\frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\frac{{{e^{inx}} + {e^{ - inx}}}}{2} + {b_n}\frac{{{e^{inx}} - {e^{ - inx}}}}{{2i}}} \right)} } = {\frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\frac{{{a_n} - i{b_n}}}{2}{e^{inx}}} + \sum\limits_{n = 1}^\infty {\frac{{{a_n} + i{b_n}}}{2}{e^{ - inx}}} } = {\sum\limits_{n = - \infty }^\infty {{c_n}{e^{inx}}} .} \] Мы использовали здесь следующие обозначения: \[ {{c_0} = \frac{{{a_0}}}{2},}\;\; {{c_n} = \frac{{{a_n} - i{b_n}}}{2},}\;\; {{c_{ - n}} = \frac{{{a_n} + i{b_n}}}{2}.} \] Коэффициенты \({c_n}\) называются комплексными коэффициентами Фурье. Они определяются формулами \[{c_n} = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {f\left( x \right){e^{ - inx}}dx} ,\;\;n = 0, \pm 1, \pm 2, \ldots \] Если нужно построить продолжение функции \(f\left( x \right),\) имеюшей произвольный период \(2L,\) то соответствующее выражение в комплексной форме имеет вид: \[f\left( x \right) = \sum\limits_{n = - \infty }^\infty {{c_n}{e^{\frac{{in\pi x}}{L}}}} ,\] где \[{c_n} = \frac{1}{{2L}}\int\limits_{ - L}^L {f\left( x \right){e^{ - \frac{{in\pi x}}{L}}}dx} ,\;\;n = 0, \pm 1, \pm 2, \ldots \] Комплексная форма ряда Фурье алгебраически проще и более симметрична. Поэтому, она часто используется в физике и прикладных расчетах.

   Пример 1

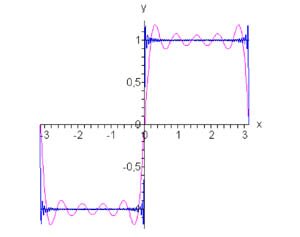
Используя комплексную форму записи, найти разложение в ряд Фурье функции \[ f\left( x \right) = \text{sign}\,x = \begin{cases} -1, & -\pi \le x \le 0 \\ 1, & 0 < x \le \pi \end{cases}. \] Вычислим коэффициенты \({c_0}\) и \({c_n}\) (при \(n \ne 0\)): \[\require{cancel} {{c_0} = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {f\left( x \right)dx} } = {\frac{1}{{2\pi }}\left[ {\int\limits_{ - \pi }^0 {\left( { - 1} \right)dx} + \int\limits_0^\pi {dx} } \right] } = {\frac{1}{{2\pi }}\left[ {\left. {\left( { - x} \right)} \right|_{ - \pi }^0 + \left. x \right|_0^\pi } \right] } = {\frac{1}{{2\pi }}\left( { - \cancel{\pi} + \cancel{\pi }} \right) = 0,} \] \[ {{c_n} = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {f\left( x \right){e^{ - inx}}dx} } = {\frac{1}{{2\pi }}\left[ {\int\limits_{ - \pi }^0 {\left( { - 1} \right){e^{ - inx}}dx} + \int\limits_0^\pi {{e^{ - inx}}dx} } \right] } = {\frac{1}{{2\pi }}\left[ { - \frac{{\left. {\left( {{e^{ - inx}}} \right)} \right|_{ - \pi }^0}}{{ - in}} + \frac{{\left. {\left( {{e^{ - inx}}} \right)} \right|_0^\pi }}{{ - in}}} \right] } = {\frac{i}{{2\pi n}}\left[ { - \left( {1 - {e^{in\pi }}} \right) + {e^{ - in\pi }} - 1} \right] } = {\frac{i}{{2\pi n}}\left[ {{e^{in\pi }} + {e^{ - in\pi }} - 2} \right] } = {\frac{i}{{\pi n}}\left[ {\frac{{{e^{in\pi }} + {e^{ - in\pi }}}}{2} - 1} \right] } = {\frac{i}{{\pi n}}\left[ {\cos n\pi - 1} \right] } = {\frac{i}{{\pi n}}\left[ {{{\left( { - 1} \right)}^n} - 1} \right].} \] Если \(n = 2k,\) то \({c_{2k}} = 0.\)
Если \(n = 2k - 1,\) то \({c_{2k - 1}} = - \large\frac{{2i}}{{\left( {2k - 1} \right)\pi }}\normalsize.\)
Следовательно, разложение в ряд Фурье в комплексной форме имеет вид: \[ {f\left( x \right) = \text{sign}\,x } = { - \frac{{2i}}{\pi }\sum\limits_{k = - \infty }^\infty {\frac{1}{{2k - 1}}{e^{i\left( {2k - 1} \right)x}}} .} \] Данный ряд можно преобразовать и записать в действительных переменных. Обозначим: \(n = 2k - 1,\;n = \pm 1, \pm 2, \pm 3, \ldots \) Тогда \[ {f\left( x \right) = \text{sign}\,x } = { - \frac{{2i}}{\pi }\sum\limits_{k = - \infty }^\infty {\frac{1}{{2k - 1}}{e^{i\left( {2k - 1} \right)x}}} } = { - \frac{{2i}}{\pi }\sum\limits_{n = - \infty }^\infty {\frac{{{e^{inx}}}}{n}} } = { - \frac{{2i}}{\pi }\sum\limits_{n = 1}^\infty {\left( {\frac{{{e^{ - inx}}}}{{ - n}} + \frac{{{e^{inx}}}}{n}} \right)} } = {\frac{4}{\pi }\sum\limits_{n = 1}^\infty {\frac{{{e^{inx}} - {e^{ - inx}}}}{{2in}}} } = {\frac{4}{\pi }\sum\limits_{n = 1}^\infty {\frac{{\sin nx}}{n}} } = {\frac{4}{\pi }\sum\limits_{k = 1}^\infty {\frac{{\sin \left( {2k - 1} \right)x}}{{2k - 1}}} .} \] График функции и ее ряд Фурье при \(n = 5\) и \(n = 50\) показаны на рисунке \(1.\)

   Пример 2

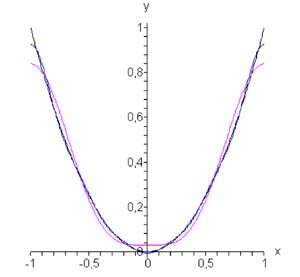
Найти разложение в ряд Фурье в комплексной форме для функции \(f\left( x \right) = {x^2},\) заданной в интервале \(\left[ { - 1,1} \right].\) Здесь полупериод равен \(L = 1.\) Поэтому \({c_0}\) равен \[ {{c_0} = \frac{1}{{2L}}\int\limits_{ - L}^L {f\left( x \right)dx} } = {\frac{1}{2}\int\limits_{ - 1}^1 {{x^2}dx} } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_{ - 1}^1} \right] } = {\frac{1}{6}\left[ {{1^3} - {{\left( { - 1} \right)}^3}} \right] } = {\frac{1}{3}.} \] Для \(n \ne 0\) получаем \[ {{c_n} = \frac{1}{{2L}}\int\limits_{ - L}^L {f\left( x \right){e^{ - \frac{{in\pi x}}{L}}}dx} } = {\frac{1}{2}\int\limits_{ - 1}^1 {{x^2}{e^{ - {in\pi x}}}dx} .} \] Дважды интегрируя по частям, находим \[ {{c_n} = \frac{1}{2}\left[ {\left. {\left( {\frac{{{x^2}{e^{ - in\pi x}}}}{{ - in\pi }}} \right)} \right|_{ - 1}^1 - \int\limits_{ - 1}^1 {\frac{{2x{e^{ - in\pi x}}}}{{ - in\pi }}dx} } \right] } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{{x^2}{e^{ - in\pi x}}}}{{ - in\pi }}} \right)} \right|_{ - 1}^1 + \frac{2}{{in\pi }}\int\limits_{ - 1}^1 {x{e^{ - in\pi x}}dx} } \right] } = {\frac{1}{2}\left\{ {\left. {\left( {\frac{{{x^2}{e^{ - in\pi x}}}}{{ - in\pi }}} \right)} \right|_{ - 1}^1 + \frac{2}{{in\pi }}\left[ {\left. {\left( {\frac{{x{e^{ - in\pi x}}}}{{ - in\pi }}} \right)} \right|_{ - 1}^1 - \int\limits_{ - 1}^1 {\frac{{{e^{ - in\pi x}}}}{{ - in\pi }}dx} } \right]} \right\} } = { - \frac{1}{{2in\pi }}\left[ {\left. {\left( {{x^2}{e^{ - in\pi x}} + \frac{2}{{in\pi }}x{e^{ - in\pi x}} + \frac{2}{{{{\left( {in\pi } \right)}^2}}}{e^{ - in\pi x}}} \right)} \right|_{ - 1}^1} \right] } = {- \frac{1}{{2in\pi }}\left[ {{e^{ - in\pi }} + \frac{2}{{in\pi }}{e^{ - in\pi }} + \frac{2}{{{{\left( {in\pi } \right)}^2}}}{e^{ - in\pi }}} \right. } + {\left. {\frac{2}{{in\pi }}{e^{in\pi }} - \frac{2}{{{{\left( {in\pi } \right)}^2}}}{e^{in\pi }}} \right] } = {\frac{1}{{2in\pi }}\left[ {{e^{in\pi }} - {e^{ - in\pi }} - \frac{2}{{in\pi }}\left( {{e^{in\pi }} + {e^{ - in\pi }}} \right)} \right. } + {\left. {\frac{2}{{{{\left( {in\pi } \right)}^2}}}\left( {{e^{in\pi }} - {e^{ - in\pi }}} \right)} \right] } = {\frac{1}{{n\pi }} \cdot \frac{{{e^{in\pi }} - {e^{ - in\pi }}}}{{2i}} } + {\frac{2}{{{n^2}{\pi ^2}}} \cdot \frac{{{e^{in\pi }} + {e^{ - in\pi }}}}{2} } - {\frac{2}{{{n^3}{\pi ^3}}} \cdot \frac{{{e^{in\pi }} - {e^{ - in\pi }}}}{{2i}} } = {\frac{1}{{n\pi }} \cdot \sin n\pi + \frac{2}{{{n^2}{\pi ^2}}}\cos n\pi - \frac{2}{{{n^3}{\pi ^3}}}\sin n\pi .} \] Подставляя \(\sin n\pi = 0\) и \(\cos n\pi = {\left( { - 1} \right)^n},\) получаем компактное выражение для коэффициентов \({c_n}:\) \[{c_n} = \frac{2}{{{n^2}{\pi ^2}}}{\left( { - 1} \right)^n}.\] Таким образом, разложение в ряд Фурье в комплексной форме имеет вид \[ {f\left( x \right) = {x^2} } = {\frac{1}{3} + \sum\limits_{n = 1}^\infty {\frac{2}{{{n^2}{\pi ^2}}}{{\left( { - 1} \right)}^n}{e^{in\pi x}}} } + {\sum\limits_{n = 1}^\infty {\frac{2}{{{{\left( { - n} \right)}^2}{\pi ^2}}}{{\left( { - 1} \right)}^{ - n}}{e^{ - in\pi x}}} .} \] Учитывая, что \({\left( { - 1} \right)^{ - n}} = {\left( { - 1} \right)^n},\) можно окончательно записать \[ {f\left( x \right) = {x^2} } = {\frac{1}{3} + \frac{4}{{{\pi ^2}}}\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\frac{{{e^{in\pi x}} + {e^{ - in\pi x}}}}{2}} } = {\frac{1}{3} + \frac{4}{{{\pi ^2}}}\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos n\pi x} .} \] График данной функции и ее аппроксимации Фурье приведены ни рисунке \(2\) (выше).

   Пример 3

Используя комплексную форму записи, найти ряд Фурье для функции \[f\left( x \right) = \frac{{a\sin x}}{{1 - 2a\cos x + {a^2}}},\;\;\left| a \right| < 1.\] Применим формулы \[ {\cos x = \frac{{{e^{ix}} + {e^{ - ix}}}}{2},}\;\; {\sin x = \frac{{{e^{ix}} - {e^{ - ix}}}}{{2i}}.} \] В результате функция принимает вид \[ {f\left( x \right) = \frac{{a \cdot \frac{{{e^{ix}} - {e^{ - ix}}}}{{2i}}}}{{1 - 2a \cdot \frac{{{e^{ix}} + {e^{ - ix}}}}{2} + {a^2}}} } = {\frac{1}{{2i}} \cdot \frac{{a\left( {{e^{ix}} - {e^{ - ix}}} \right)}}{{1 - a\left( {{e^{ix}} + {e^{ - ix}}} \right) + {a^2}}} } = {\frac{1}{{2i}} \cdot \frac{{a\left( {{e^{ix}} - {e^{ - ix}}} \right)}}{{1 - a{e^{ix}} - a{e^{ - ix}} + {a^2}{e^{ix}}{e^{ - ix}}}} } = {\frac{1}{{2i}} \cdot \frac{{a\left( {{e^{ix}} - {e^{ - ix}}} \right)}}{{\left( {1 - a{e^{ix}}} \right) - a{e^{ - ix}}\left( {1 - a{e^{ix}}} \right)}} } = {\frac{1}{{2i}} \cdot \frac{{a\left( {{e^{ix}} - {e^{ - ix}}} \right)}}{{\left( {1 - a{e^{ix}}} \right)\left( {1 - a{e^{ - ix}}} \right)}}.} \] Разложим последнее выражение на сумму простых рациональных дробей. \[ {f\left( x \right) = \frac{1}{{2i}} \cdot \frac{{a\left( {{e^{ix}} - {e^{ - ix}}} \right)}}{{\left( {1 - a{e^{ix}}} \right)\left( {1 - a{e^{ - ix}}} \right)}} } = {\frac{1}{{2i}}\left( {\frac{A}{{1 - a{e^{ix}}}} + \frac{B}{{1 - a{e^{ - ix}}}}} \right).} \] Определим коэффициенты \(A, B:\) \[ {A\left( {1 - a{e^{ - ix}}} \right) + B\left( {1 - a{e^{ix}}} \right) = a{e^{ix}} - a{e^{ - ix}},}\;\; {\Rightarrow A - aA{e^{ - ix}} + B - aB{e^{ix}} = a{e^{ix}} - a{e^{ - ix}},}\;\; {\Rightarrow A = 1,\;B = - 1.} \] В результате функцию \(f\left( x \right)\) можно записать в виде \[f\left( x \right) = \frac{1}{{2i}}\left( {\frac{1}{{1 - a{e^{ix}}}} - \frac{1}{{1 - a{e^{ - ix}}}}} \right).\] При этом \[ {\left| {a{e^{ix}}} \right| = \left| a \right|\left| {{e^{ix}}} \right| } = {\left| a \right|\sqrt {{{\cos }^2}x + {{\sin }^2}x} } = {\left| a \right| < 1.} \] И такой же результат справедлив для сопряженного выражения: \[\left| {a{e^{ - ix}}} \right| = \left| {a{e^{ix}}} \right| = \left| a \right| < 1.\] Представляя дроби в виде степенных рядов, получаем \[\frac{1}{{1 - a{e^{ix}}}} = {\left( {1 - a{e^{ix}}} \right)^{ - 1}} = \sum\limits_{n = 0}^\infty {{a^n}{e^{inx}}} ,\] \[\frac{1}{{1 - a{e^{ - ix}}}} = {\left( {1 - a{e^{ - ix}}} \right)^{ - 1}} = \sum\limits_{n = 0}^\infty {{a^n}{e^{ - inx}}} .\] Таким образом, разложение функции \(f\left( x \right)\) в ряд Фурье имеет вид \[ {f\left( x \right) = \frac{1}{{2i}}\sum\limits_{n = 0}^\infty {{a^n}\left( {{e^{inx}} - {e^{ - inx}}} \right)} } = {\sum\limits_{n = 0}^\infty {{a^n}\sin nx} .} \] Поскольку \(\sin nx = 0\) при \(n = 0,\) то окончательный ответ будет \[f\left( x \right) = \sum\limits_{n = 1}^\infty {{a^n}\sin nx} .\]