Классические неравенства

Среди неравенств выделяют ряд известных классических неравенств. Многие из них были доказаны знаменитыми математиками и названы их именами. К ним, в частности, относятся неравенства Бернулли, Юнга, Гельдера, Коши, Минковского (конечно, это далеко не полный список). Соотношения между основными классическими неравенствами можно представить в виде древовидной диаграммы (рисунок \(1\)), из которой видно, что, например, неравенство Коши следует из неравенства Гельдера и т.д. Далее мы подробнее рассмотрим каждое из неравенств, указанное на диаграмме. Источником для вывода многих классических неравенств служит простое соотношение вида \[{\left( {1 + x} \right)^\alpha } \le 1 + \alpha x,\] где \(x \ge -1,\) \(0 < \alpha < 1.\)

Данное неравенство можно доказать с помощью производной. Рассмотрим функцию \[f\left( x \right) = {\left( {1 + x} \right)^\alpha } - \alpha x - 1\] при условии \(x \ge -1.\) Дифференцируя ее, получаем \[ {f'\left( x \right) = {\left[ {{{\left( {1 + x} \right)}^\alpha } - \alpha x - 1} \right]^\prime } } = {\alpha {\left( {1 + x} \right)^{\alpha - 1}} - \alpha } = {\alpha \left[ {{{\left( {1 + x} \right)}^{\alpha - 1}} - 1} \right].} \] Видно, что производная равна нулю при \(x = 0.\) Знак производной слева и справа от точки \(x = 0\) зависит от значения \(\alpha:\)

1. При \(0 < \alpha < 1\) производная \(f'\left( x \right)\) при переходе через точку \(x = 0\) меняет знак с плюса на минус. В этом случае мы имеем максимум в точке \(x = 0.\)

2. При \(\alpha < 0\) или \(\alpha > 1\) производная \(f'\left( x \right)\) при переходе через точку \(x = 0\) меняет знак с минуса на плюс. Следовательно, эта точка является точкой минимума.

Таким образом, при \(x > -1\) функция \(f\left( x \right)\) в случае \(1\) является убывающей, а в случае \(2\) − возрастающей. Учтем, что функция \(f\left( x \right)\) равна нулю в точке \(x = 0.\) Тогда справедливы следующие неравенства при условии \(x \ge -1:\)

1. \(f\left( x \right) \le 0\)  при  \(0 < \alpha < 1\);

2. \(f\left( x \right) \ge 0\)  при  \(\alpha < 0\)  или  \(\alpha > 1\);

или

1. \({\left( {1 + x} \right)^\alpha } - \alpha x - 1 \le 0\)  при  \(0 < \alpha < 1\);

2. \({\left( {1 + x} \right)^\alpha } - \alpha x - 1 \ge 0\)  при  \(\alpha < 0\)  или  \(\alpha > 1\).

В первом случае (при \(0 < \alpha < 1\)) полученное неравенство можно записать как \[{\left( {1 + x} \right)^\alpha } \le \alpha x + 1.\] Это соотношение используется для доказательства других классических неравенств.

Во втором случае (при \(\alpha < 0\) или \(\alpha > 1\)) неравенство можно представить в виде \[{\left( {1 + x} \right)^\alpha } \ge \alpha x + 1.\] В частном случае, если считать, что \(\alpha\) − натуральный показатель, мы получаем известное неравенство Бернулли: \[{\left( {1 + x} \right)^n} \ge 1 + nx,\;\;\text{где}\;\;x \ge - 1,\;n \in \mathbb{N}.\] Запишем снова полученное выше неравенство \[{\left( {1 + x} \right)^\alpha } \le \alpha x + 1,\] которое справедливо при \(x \ge -1,\) \(0 < \alpha < 1.\) Введем следующие обозначения: \[ {1 + x = \frac{a}{b},}\;\;\; {\alpha = \frac{1}{p},}\;\;\; {\frac{1}{q} = 1 - \frac{1}{p}.} \] Здесь предполагается, что \(a \ge 0,\) \(b > 0.\) Из условия \(0 < \alpha < 1\) вытекает также, что \(p > 1.\) Подставляя это в наше неравенство, имеем: \[ {{\left( {\frac{a}{b}} \right)^{\large\frac{1}{p}\normalsize}} \le 1 + \frac{1}{p}\left( {\frac{a}{b} - 1} \right),}\;\; {\Rightarrow \frac{{{a^{\large\frac{1}{p}\normalsize}}}}{{{b^{\large\frac{1}{p}\normalsize}}}} \le 1 - \frac{1}{p} + \frac{1}{p}\frac{a}{b},}\;\; {\Rightarrow \frac{{{a^{\large\frac{1}{p}\normalsize}}}}{{{b^{\large\frac{1}{p}\normalsize}}}} \le \frac{1}{q} + \frac{1}{p}\frac{a}{b}.} \] Умножим обе части на \(b\) (\(b > 0\)). Следовательно, \[ {{a^{\large\frac{1}{p}\normalsize}}{b^{1 - \large\frac{1}{p}\normalsize}} \le \frac{a}{p} + \frac{b}{q},}\;\; {\Rightarrow {a^{\large\frac{1}{p}\normalsize}}{b^{\large\frac{1}{q}\normalsize}} \le \frac{a}{p} + \frac{b}{q}.} \] Мы получили неравенство Юнга.

Если переобозначить \({a^{\large\frac{1}{p}\normalsize}} \to a,\) \({b^{\large\frac{1}{q}\normalsize}} \to b,\) то неравенство Юнга можно записать в таком виде: \[ab \le \frac{{{a^p}}}{p} + \frac{{{b^q}}}{q}\;\;\left( {p > 1} \right).\] Заметим, что при \(p < 1\) неравенство Юнга записывается с противоположным знаком: \[ab \ge \frac{{{a^p}}}{p} + \frac{{{b^q}}}{q}\;\;\left( {p < 1,\,p \ne 0} \right).\] При \(p = q = \large\frac{1}{2}\normalsize\) из неравенства Юнга вытекает соотношение между средним геометрическим и средним арифметическим двух положительных чисел: \[ {{a^{\large\frac{1}{2}\normalsize}}{b^{\large\frac{1}{2}\normalsize}} \le \frac{a}{2} + \frac{b}{2}}\;\; {\text{или}\;\;\sqrt {ab} \le \frac{{a + b}}{2}.} \] На самом деле, неравенство Юнга можно обобщить на случай \(n\) чисел. Тогда оно принимает такой вид: \[ {a_1^{\large\frac{1}{{{p_1}}}\normalsize}a_2^{\large\frac{1}{{{p_2}}}\normalsize} \ldots a_n^{\large\frac{1}{{{p_n}}}\normalsize} } {\le \frac{{{a_1}}}{{{p_1}}} + \frac{{{a_2}}}{{{p_2}}} + \ldots + \frac{{{a_n}}}{{{p_n}}},} \] где \[ {{a_1},{a_2}, \ldots ,{a_n},{p_1},{p_2}, \ldots ,{p_n} > 0,}\;\;\; {\frac{1}{{{p_1}}} + \frac{1}{{{p_2}}} + \ldots + \frac{1}{{{p_n}}} = 1.} \] Полагая \({p_1} = {p_2} = \ldots = {p_n} = n,\) приходим к соотношению \[\sqrt[\large n\normalsize]{{{a_1}{a_2} \cdots {a_n}}} \le \frac{{{a_1} + {a_2} + \ldots + {a_n}}}{n},\] которое означает, что среднее геометрическое \(n\) положительных чисел не превосходит их среднего арифметического. Рассмотрим \(n\) пар положительных чисел \({x_i},{y_i},\,\left( {i = 1, \ldots ,n} \right).\) Если числа \(p\) и \(q\) удовлетворяют условию \(\large\frac{1}{p}\normalsize + \large\frac{1}{q}\normalsize = 1,\) то справедливо неравенство Гельдера, которое при \(p > 1\) имеет вид \[ {\sum\limits_{i = 1}^n {{a_i}{b_i}} } {\le {\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)^{\large\frac{1}{p}\normalsize}}{\left( {\sum\limits_{i = 1}^n {b_i^q} } \right)^{\large\frac{1}{q}\normalsize}}.} \] Докажем это соотношение. Введем обозначения: \[ {A = \sum\limits_{i = 1}^n {a_i^p} ,}\;\;\; {B = \sum\limits_{i = 1}^n {b_i^q}.} \] Тогда неравенство Гельдера записывается таким образом: \[\sum\limits_{i = 1}^n {{a_i}{b_i}} \le {A^{\large\frac{1}{p}\normalsize}}{B^{\large\frac{1}{q}\normalsize}}.\] Воспользуемся далее неравенством Юнга в виде \[{a^{\large\frac{1}{p}\normalsize}}{b^{\large\frac{1}{q}\normalsize}} \le \frac{a}{p} + \frac{b}{q}.\] Пусть \[a = \frac{{a_i^p}}{A},\;\;\;b = \frac{{b_i^q}}{B}.\] Применяя неравенство Юнга к каждой паре чисел \({a_i}\) и \({b_i},\) получаем: \[\require{cancel} {\sum\limits_{i = 1}^n {\frac{{{a_i}{b_i}}}{{{A^{\large\frac{1}{p}\normalsize}}{B^{\large\frac{1}{q}\normalsize}}}}} \le \sum\limits_{i = 1}^n {\left( {\frac{{a_i^p}}{{pA}} + \frac{{b_i^q}}{{qB}}} \right)} ,}\;\; {\Rightarrow \frac{{\sum\limits_{i = 1}^n {{a_i}{b_i}} }}{{{A^{\large\frac{1}{p}\normalsize}}{B^{\large\frac{1}{q}\normalsize}}}} \le \frac{{\sum\limits_{i = 1}^n {a_i^p} }}{{pA}} + \frac{{\sum\limits_{i = 1}^n {b_i^q} }}{{qB}},}\;\; {\Rightarrow \frac{{\sum\limits_{i = 1}^n {{a_i}{b_i}} }}{{{A^{\large\frac{1}{p}\normalsize}}{B^{\large\frac{1}{q}\normalsize}}}} \le \frac{\cancel{A}}{{p\cancel{A}}} + \frac{\cancel{B}}{{q\cancel{B}}} = \frac{1}{p} + \frac{1}{q} = 1,}\;\; {\Rightarrow \sum\limits_{i = 1}^n {{a_i}{b_i}} \le {A^{\large\frac{1}{p}\normalsize}}{B^{\large\frac{1}{q}\normalsize}},}\;\; {\Rightarrow \sum\limits_{i = 1}^n {{a_i}{b_i}} \le {\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)^{\large\frac{1}{p}\normalsize}}{\left( {\sum\limits_{i = 1}^n {b_i^q} } \right)^{\large\frac{1}{q}\normalsize}}\;\;\left( {p > 1} \right).} \] Таким образом, неравенство Гельдера доказано для случая \(p > 1.\) При \(p < 1\) (\(p \ne 0\)) это неравенство записывается с противоположным знаком: \[ {\sum\limits_{i = 1}^n {{a_i}{b_i}} \ge {\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)^{\large\frac{1}{p}\normalsize}}{\left( {\sum\limits_{i = 1}^n {b_i^q} } \right)^{\large\frac{1}{q}\normalsize}}}\;\; {\left( {p < 1,\,p \ne 0} \right).} \] Еще одно известное соотношение − неравенство Коши − представляет собой частный случай неравенства Гельдера при \(p = q = 2.\) Оно записывается в виде \[\sum\limits_{i = 1}^n {{a_i}{b_i}} \le \sqrt {\sum\limits_{i = 1}^n {a_i^2} } \sqrt {\sum\limits_{i = 1}^n {b_i^2} } .\] Согласно неравенству Минковского, для положительных чисел \({a_i}\) и \({b_i}\) справедливо следующее соотношение: \[ {{\left( {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^p}} } \right)^{\large\frac{1}{p}\normalsize}} }\kern0pt {\le {\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)^{\large\frac{1}{p}\normalsize}} }\kern0pt {+ {\left( {\sum\limits_{i = 1}^n {b_i^p} } \right)^{\large\frac{1}{p}\normalsize}},} \] где \(p > 1.\)

Это неравенство также выводится из формулы Гельдера, рассмотренной выше. Представим сумму в левой части неравенства Минковского таким образом: \[ {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^p}} } = {\sum\limits_{i = 1}^n {\left( {{a_i} + {b_i}} \right){{\left( {{a_i} + {b_i}} \right)}^{p - 1}}} } = {\sum\limits_{i = 1}^n {{a_i}{{\left( {{a_i} + {b_i}} \right)}^{p - 1}}} } + {\sum\limits_{i = 1}^n {{b_i}{{\left( {{a_i} + {b_i}} \right)}^{p - 1}}} .} \] К каждой из полученных сумм применим неравенство Гельдера. Тогда \[ {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^p}} = \sum\limits_{i = 1}^n {{a_i}{{\left( {{a_i} + {b_i}} \right)}^{p - 1}}} }\kern0pt {+ \sum\limits_{i = 1}^n {{b_i}{{\left( {{a_i} + {b_i}} \right)}^{p - 1}}} }\kern0pt {\le {\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)^{\large\frac{1}{p}\normalsize}}{\left( {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^{\left( {p - 1} \right)q}}} }\kern0pt \right)^{\large\frac{1}{q}\normalsize}} }\kern0pt {+ {\left( {\sum\limits_{i = 1}^n {b_i^p} } \right)^{\large\frac{1}{p}\normalsize}}{\left( {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^{\left( {p - 1} \right)q}}} }\kern0pt \right)^{\large\frac{1}{q}\normalsize}} }\kern0pt = {\left[ {{{\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)}^{\large\frac{1}{p}\normalsize}} + {{\left( {\sum\limits_{i = 1}^n {b_i^p} } \right)}^{\large\frac{1}{p}\normalsize}}}\kern0pt \right]{\left( {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^{\left( {p - 1} \right)q}}} } \right)^{\large\frac{1}{q}\normalsize}}.} \] Учтем, что здесь \[ {\frac{1}{p} + \frac{1}{q} = 1,}\;\; {\Rightarrow \frac{1}{q} = 1 - \frac{1}{p} = \frac{{p - 1}}{p},}\;\; {\Rightarrow q = \frac{p}{{p - 1}}.} \] Следовательно, предыдущее выражение можно представить так: \[ {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^p}} } {\le \left[ {{{\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)}^{\large\frac{1}{p}\normalsize}} + {{\left( {\sum\limits_{i = 1}^n {b_i^p} } \right)}^{\large\frac{1}{p}\normalsize}}} \right]{\left( {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^p}} } \right)^{\large\frac{1}{q}\normalsize}},}\;\; {\Rightarrow \frac{{\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^p}} }}{{{{\left( {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^p}} } \right)}^{\large\frac{1}{q}\normalsize}}}} } {\le {\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)^{\large\frac{1}{p}\normalsize}} + {\left( {\sum\limits_{i = 1}^n {b_i^p} } \right)^{\large\frac{1}{p}\normalsize}}.} \] Поскольку \(1 - \large\frac{1}{q}\normalsize = \large\frac{1}{p}\normalsize,\) то в результате приходим к неравенству Минковского: \[ {{\left( {\sum\limits_{i = 1}^n {{{\left( {{a_i} + {b_i}} \right)}^p}} } \right)^{\large\frac{1}{p}\normalsize}} } {\le {\left( {\sum\limits_{i = 1}^n {a_i^p} } \right)^{\large\frac{1}{p}\normalsize}} } {+ {\left( {\sum\limits_{i = 1}^n {b_i^p} } \right)^{\large\frac{1}{p}\normalsize}}.} \] Соответственно, в случае \(p < 1\) (\(p \ne 0\)) неравенство Минковского записывается с противоположным знаком. 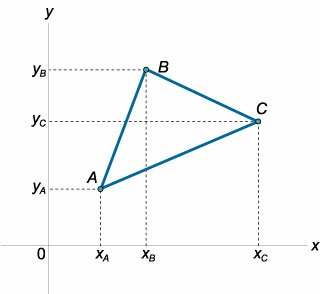Неравенство треугольника на плоскости следует из неравенства Минковского при \(n = 2,\) \(p = 2.\)

Рассмотрим на плоскости треугольник \(ABC\) (рисунок \(7\)), координаты вершин которого составляют \(A\left( {{x_A},{y_A}} \right),\) \(B\left( {{x_B},{y_B}} \right),\) \(C\left( {{x_C},{y_C}} \right).\) Подставляя значения \(n = 2,\) \(p = 2\) в формулу Минковского, получаем: \[ {\sqrt {\sum\limits_{i = 1}^2 {{{\left( {{a_i} + {b_i}} \right)}^2}} } } {\le \sqrt {\sum\limits_{i = 1}^2 {a_i^2} } + \sqrt {\sum\limits_{i = 1}^2 {b_i^2} } ,}\;\; {\Rightarrow \sqrt {{{\left( {{a_1} + {b_1}} \right)}^2} + {{\left( {{a_2} + {b_2}} \right)}^2}} } {\le \sqrt {a_1^2 + a_2^2} + \sqrt {b_1^2 + b_2^2} .} \] Пусть числа \({a_1},{a_2},{b_1},{b_2}\) выражаются через координаты вершин таким образом: \[ {{a_1} = {x_A} - {x_B},}\;\;\; {{a_2} = {y_A} - {y_B},}\;\;\; {{b_1} = {x_B} - {x_C},}\;\;\; {{b_2} = {y_B} - {y_C}.} \] Следовательно, можно записать: \[ {\sqrt {{{\left( {{x_A} - \cancel{x_B} + \cancel{x_B} - {x_C}} \right)}^2} + {{\left( {{y_A} - \cancel{y_B} + \cancel{y_B} - {y_C}} \right)}^2}} }\kern0pt {\le \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} }\kern0pt {+ \sqrt {{{\left( {{x_B} - {x_C}} \right)}^2} + {{\left( {{y_B} - {y_C}} \right)}^2}} } \] или \[ {\sqrt {{{\left( {{x_A} - {x_C}} \right)}^2} + {{\left( {{y_A} - {y_C}} \right)}^2}} } {\le \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} } {+ \sqrt {{{\left( {{x_B} - {x_C}} \right)}^2} + {{\left( {{y_B} - {y_C}} \right)}^2}} .} \] Это неравенство называется неравенством треугольника и описывает соотношение между длинами сторон треугольника: \[\left| {AC} \right| \le \left| {AB} \right| + \left| {BC} \right|.\] Оно означает, что длина любой стороны треугольника не превосходит сумму длин двух его других сторон. Знак равенства при этом возможен лишь в случае, когда три точки лежат на одной прямой.

Аналогично из неравенства Минковского можно получить неравенство треугольника в трехмерном Евклидовом пространстве. Этот случай реализуется при \(n = 3,\) \(p = 2.\)