Замена переменных в двойных интегралах

Для вычисления двойного интеграла \(\iint\limits_R {f\left( {x,y} \right)dxdy}\) иногда удобнее перейти в другую систему координат. Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции. В новой системе координат вычисление двойного интеграла значительно упрощается.

Замена переменных в двойном интеграле описывается формулой \[ {\iint\limits_R {f\left( {x,y} \right)dxdy} } = {\iint\limits_S {f\left[ {x\left( {u,v} \right),y\left( {u,v} \right)} \right]\left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right|dxdy} ,} \] где выражение \(\left| {\large\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}\normalsize} \right| = \left| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial u}}}&{\frac{{\partial x}}{{\partial v}}}\\ {\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial y}}{{\partial v}}} \end{array}} \right| \ne 0\) представляет собой так называемый якобиан преобразования \(\left( {x,y} \right) \to \left( {u,v} \right),\) а \(S\) − образ области интегрирования \(R,\) который можно найти с помощью подстановки \(x = x\left( {u,v} \right),\) \(y = y\left( {u,v} \right)\) в определение области \(R.\) Отметим, что в приведенной выше формуле \(\left| {\large\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}\normalsize} \right|\) означает абсолютное значение соответствующего определителя.

В предположении, что преобразование \(\left( {x,y} \right) \to \left( {u,v} \right)\) является взаимно-однозначным, соотношение между якобианами прямого и обратного преобразования координат записывается в виде \[\left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right| = \left| {{{\left( {\frac{{\partial \left( {u,v} \right)}}{{\partial \left( {x,y} \right)}}} \right)}^{ - 1}}} \right|\] при условии, что знаменатель нигде не равен \(0.\)

Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:

1. Найти образ \(S\) в новой системе координат \(\left( {u,v} \right)\) для исходной области интегрирования \(R;\)

2. Вычислить якобиан преобразования \(\left( {x,y} \right) \to \left( {u,v} \right)\) и записать дифференциал в новых переменных \(dxdy = \left| {\large\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}\normalsize} \right|dudv;\)

3. Заменить в подынтегральном выражении исходные переменные \(x\) и \(y,\) выполнив, соответственно, подстановки \(x = x\left( {u,v} \right)\) и \(y = y\left( {u,v} \right).\)

   Пример 1

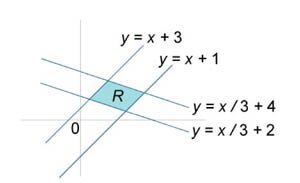
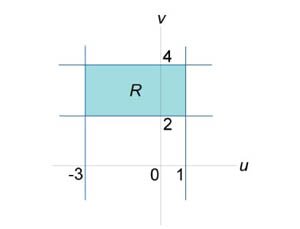
Вычислить двойной интеграл \(\iint\limits_R {\left( {y - x} \right)dxdy},\) в котором область определения \(R\) ограничена прямыми \(y = x + 1,\) \(y = x - 3,\) \(y = - \large\frac{x}{3}\normalsize + 2,\) \(y = - \large\frac{x}{3}\normalsize + 4.\) Область \(R\) схематически показана на рисунке \(1.\) Для упрощения интеграла выполним замену переменных. Полагая \(u = y - x,\) \(v = y + \large\frac{x}{3}\normalsize,\) получаем \[ {y = x + 1,}\;\; {\Rightarrow y - x = 1,}\;\; {\Rightarrow u = 1,} \] \[ {y = x - 3,}\;\; {\Rightarrow y - x = -3,}\;\; {\Rightarrow u = -3,} \] \[ {y = - \frac{x}{3} + 2,}\;\; {\Rightarrow y + \frac{x}{3} = 2,}\;\; {\Rightarrow v = 2,} \] \[ {y = - \frac{x}{3} + 4,}\;\; {\Rightarrow y + \frac{x}{3} = 4,}\;\; {\Rightarrow v = 4.} \] Следовательно, образ \(S\) области \(R\) имеет вид прямоугольника, как показано на рисунке \(2.\) Определим якобиан данного преобразования. Сначала вычислим определитель обратного преобразования: \[ {\frac{{\partial \left( {u,v} \right)}}{{\partial \left( {x,y} \right)}} = \left| {\begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial x}}}&{\frac{{\partial u}}{{\partial y}}}\\ {\frac{{\partial v}}{{\partial x}}}&{\frac{{\partial v}}{{\partial y}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial \left( {y - x} \right)}}{{\partial x}}}&{\frac{{\partial \left( {y - x} \right)}}{{\partial y}}}\\ {\frac{{\partial \left( {y + \frac{x}{3}} \right)}}{{\partial x}}}&{\frac{{\partial \left( {y + \frac{x}{3}} \right)}}{{\partial y}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} { - 1}&1\\ {\frac{1}{3}}&1 \end{array}} \right| } = { - 1 \cdot 1 - 1 \cdot \frac{1}{3} = - \frac{4}{3}.} \] Тогда якобиан равен \[ {\left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right| } = {\left| {{{\left( {\frac{{\partial \left( {u,v} \right)}}{{\partial \left( {x,y} \right)}}} \right)}^{ - 1}}} \right| } = {\left| {\frac{1}{{ - \frac{4}{3}}}} \right| = \frac{3}{4}.} \] Следовательно, дифференциал преобразуется следующим образом: \[ {dxdy = \left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right|dudv } = {\frac{3}{4}dudv.} \] В новых переменных \(\left( {u,v} \right)\) интеграл вычисляется намного легче: \[ {\iint\limits_R {\left( {y - x} \right)dxdy} } = {\iint\limits_S {\left( u \cdot \frac{3}{4}dudv \right)} } = {\frac{3}{4}\int\limits_{ - 3}^1 {udu} \int\limits_2^4 {dv} } = {\frac{3}{4}\left. {\left( {\frac{{{u^2}}}{2}} \right)} \right|_{ - 3}^1 \cdot \left. v \right|_2^4 } = {\frac{3}{4}\left( {\frac{1}{2} - \frac{9}{2}} \right) \cdot \left( {4 - 2} \right) = - 6.} \]

   Пример 2

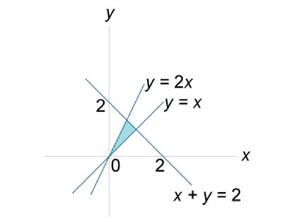
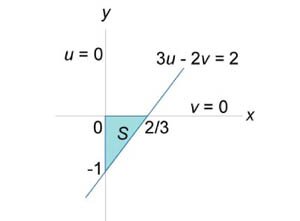
Вычислить двойной интеграл \(\iint\limits_R {\left( {x + y} \right)dxdy},\) в котором область интегрирования \(R\) ограничена прямыми линиями \(y = x,\) \(y = 2x,\) \(x + y = 2.\) Область интегрирования \(R\) имеет вид неправильного треугольника и показана на рисунке \(3.\) Чтобы упростить ее, введем новые переменные: \(y - x = u,\) \(y - 2x = v.\) Выразим \(x, y\) через \(u, v\) и определим образ области интегрирования \(S\) в новой системе координат. Легко видеть, что \[ {y = x,}\;\; {\Rightarrow y - x = 0,}\;\; {\Rightarrow u = 0,} \] \[ {y = 2x,}\;\; {\Rightarrow y - 2x = 0,}\;\; {\Rightarrow v = 0.} \] Заметим, что \[ {u - v } = {\left( {y - x} \right) - \left( {y - 2x} \right) = x.} \] Следовательно, \[ {y = x + u } = {u - v + u } = {2u - v.} \] Таким образом, мы получаем \[ {x + y = 2,}\;\; {\Rightarrow u - v + 2u - v = 2,}\;\; {\Rightarrow 3u - 2v = 2.} \] Если \(v = 0,\) то \(u = \large\frac{2}{3}\normalsize.\) Соответственно, если \(u = 0,\) то \(v = -1.\) Область \(S\) имеет вид прямоугольного треугольника (см. рисунок \(4\) выше).

Уравнение стороны \(3u - 2v = 2\) можно переписать в виде \[ {3u - 2v = 2,}\;\; {\Rightarrow v = \frac{{3u - 2}}{2} } = {\frac{3}{2}u - 1.} \] Найдем якобиан. \[ {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}} } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial u}}}&{\frac{{\partial x}}{{\partial v}}}\\ {\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial y}}{{\partial v}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial \left( {u - v} \right)}}{{\partial u}}}&{\frac{{\partial \left( {u - v} \right)}}{{\partial v}}}\\ {\frac{{\partial \left( {2u - v} \right)}}{{\partial u}}}&{\frac{{\partial \left( {2u - v} \right)}}{{\partial v}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} 1&{ - 1}\\ 2&{ - 1} \end{array}} \right| } = {1 \cdot \left( { - 1} \right) - \left( { - 1} \right) \cdot 2 = 1.} \] Следовательно, \(dxdy = dudv\) и двойной интеграл становится равным \[ {\iint\limits_R {\left( {x + y} \right)dxdy} } = {\iint\limits_S {\left( {u - v + 2u - v} \right)dudv} } = {\iint\limits_S {\left( {3u - 2v} \right)dudv} } = {\int\limits_0^{\frac{2}{3}} {\left[ {\int\limits_{\frac{3}{2}u - 1}^0 {\left( {3u - 2v} \right)dv} } \right]du} } = {\int\limits_0^{\frac{2}{3}} {\left[ {\left. {\left( {3uv - {v^2}} \right)} \right|_{v = \frac{3}{2}u - 1}^0} \right]du} } = { - \int\limits_0^{\frac{2}{3}} {\left[ {3u\left( {\frac{3}{2}u - 1} \right) - {{\left( {\frac{3}{2}u - 1} \right)}^2}} \right]du} } = { - \int\limits_0^{\frac{2}{3}} {\left( {\frac{{9{u^2}}}{2} - 3u - \frac{{9{u^2}}}{4} + 3u - 1} \right)du} } = { - \int\limits_0^{\frac{2}{3}} {\left( {\frac{{9{u^2}}}{4} - 1} \right)du} } = {\left. {\left( {u - \frac{9}{4}\frac{{{u^3}}}{3}} \right)} \right|_0^{\frac{2}{3}} } = {\frac{2}{3} - \frac{3}{4} \cdot {\left( {\frac{2}{3}} \right)^3} = \frac{4}{9}.} \]

   Пример 3

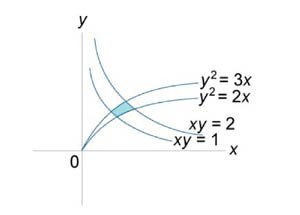
Вычислить интеграл \(\iint\limits_R {dxdy},\) где область \(R\) ограничена параболами \({y^2} = 2x,\) \({y^2} = 3x\) и гиперболами \(xy = 1,\) \(xy = 2.\) Область \(R\) схематически показана на рисунке \(5.\) Для упрощения области \(R\) сделаем замену переменных. \[ {\left\{ \begin{array}{l} u = \frac{{{y^2}}}{x}\\ v = xy \end{array} \right..} \] Образ \(S\) области \(R\) определяется следующим образом: \[ {{y^2} = 2x,}\;\; {\Rightarrow \frac{{{y^2}}}{x} = 2,}\;\; {\Rightarrow u = 2,} \] \[ {{y^2} = 3x,}\;\; {\Rightarrow \frac{{{y^2}}}{x} = 3,}\;\; {\Rightarrow u = 3,} \] \[xy = 1,\;\; \Rightarrow v = 1,\] \[xy = 2,\;\; \Rightarrow v = 2.\] Как видно, образ \(S\) является прямоугольником. Для нахождения якобиана выразим переменные \(x, y\) через \(u, v\). \[u = \frac{{{y^2}}}{x},\;\; \Rightarrow x = \frac{{{y^2}}}{u},\] \[ {v = xy,}\;\; {\Rightarrow v = \frac{{{y^2}}}{u} \cdot y,}\;\; {\Rightarrow {y^3} = uv.} \] Отсюда следует \[y = \sqrt[3]{{uv}} = {u^{\frac{1}{3}}}{v^{\frac{1}{3}}},\] \[ {x = \frac{{{y^2}}}{u} } = {\frac{{\sqrt[3]{{{u^2}{v^2}}}}}{u} } = {\sqrt[3]{{\frac{{{v^2}}}{u}}} } = {{u^{ - \frac{1}{3}}}{v^{\frac{2}{3}}}.} \] Находим якобиан данного преобразования. \[ {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}} } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial u}}}&{\frac{{\partial x}}{{\partial v}}}\\ {\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial y}}{{\partial v}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial \left( {{u^{ - \frac{1}{3}}}{v^{\frac{2}{3}}}} \right)}}{{\partial u}}}&{\frac{{\partial \left( {{u^{ - \frac{1}{3}}}{v^{\frac{2}{3}}}} \right)}}{{\partial v}}}\\ {\frac{{\partial \left( {{u^{\frac{1}{3}}}{v^{\frac{1}{3}}}} \right)}}{{\partial u}}}&{\frac{{\partial \left( {{u^{\frac{1}{3}}}{v^{\frac{1}{3}}}} \right)}}{{\partial v}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {{v^{\frac{2}{3}}}\left( { - \frac{1}{3}{u^{ - \frac{4}{3}}}} \right)}&{{u^{ - \frac{1}{3}}} \cdot \frac{2}{3}{v^{ - \frac{1}{3}}}}\\ {\frac{1}{3}{u^{ - \frac{2}{3}}}{v^{\frac{1}{3}}}}&{\frac{1}{3}{v^{ - \frac{2}{3}}}{u^{\frac{1}{3}}}} \end{array}} \right| } = { - \frac{1}{3}{u^{ - \frac{4}{3}}}{v^{\frac{2}{3}}} \cdot \frac{1}{3}{u^{\frac{1}{3}}}{v^{ - \frac{2}{3}}} } - {\frac{2}{3}{u^{ - \frac{1}{3}}}{v^{ - \frac{1}{3}}} \cdot \frac{1}{3}{u^{ - \frac{2}{3}}}{v^{\frac{1}{3}}} } = { - \frac{1}{9}{u^{ - 1}} - \frac{2}{9}{u^{ - 1}} } = { - \frac{1}{3}{u^{ - 1}} = - \frac{1}{{3u}}.} \] Соотношение между дифференциалами имеет вид \[ {dxdy = \left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right|dudv } = {\left| { - \frac{1}{{3u}}} \right|dudv } = {\frac{{dudv}}{{3u}}.} \] Теперь легко найти искомый интеграл: \[ {\iint\limits_R {dxdy} } = {\iint\limits_S {\frac{{dudv}}{{3u}}} } = {\int\limits_2^3 {\frac{{du}}{{3u}}} \int\limits_1^2 {dv} } = {\frac{1}{3}\left. {\left( {\ln u} \right)} \right|_2^3 \cdot \left. v \right|_2^3 } = {\frac{1}{3}\left( {\ln 3 - \ln 2} \right) \cdot \left( {2 - 1} \right) } = {\frac{1}{3}\ln \frac{3}{2}.} \]

   Пример 4

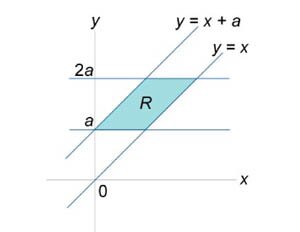
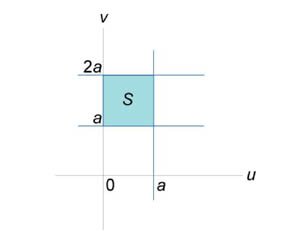
Вычислить интеграл \(\iint\limits_R {\left( {{x^2} + {y^2}} \right)dxdy},\) где область \(R\) ограничена прямыми \(y = x,\) \(y = x + a,\) \(y = a,\) \(y = 2a\;\left(a > 0\right).\) Область интегрирования \(R\) имеет форму параллелограмма и показана на рисунке \(6.\) Сделаем следующую замену переменных: \[ {\left\{ \begin{array}{l} u = y - x\\ v = y \end{array} \right.}\;\; {\text{или}\;\;\left\{ \begin{array}{l} x = y - u = v - u\\ y = v \end{array} \right..} \] Цель этой замены − упростить область интегрирования \(R.\)
Найдем образ \(S\) области \(R\) в новых координатах \(\left( {u,v} \right).\) \[ {y = x,}\;\; {\Rightarrow y - x = 0,}\;\; {\Rightarrow u = 0,} \] \[ {y = x + a,}\;\; {\Rightarrow y - x = a,}\;\; {\Rightarrow u = a,} \] \[y = a,\;\; \Rightarrow v = a,\] \[y = 2a,\;\; \Rightarrow v = 2a.\] Из рисунка \(7\) видно, что область \(S\) представляет собой прямоугольник. Вычислим якобиан. \[ {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}} } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial u}}}&{\frac{{\partial x}}{{\partial v}}}\\ {\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial y}}{{\partial v}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial \left( {v - u} \right)}}{{\partial u}}}&{\frac{{\partial \left( {v - u} \right)}}{{\partial v}}}\\ {\frac{{\partial v}}{{\partial u}}}&{\frac{{\partial v}}{{\partial v}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} { - 1}&1\\ 0&1 \end{array}} \right| } = { - 1 \cdot 1 - 1 \cdot 0 = - 1,} \] так что \[ {dxdy = \left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right|dudv } = {\left| { - 1} \right| \cdot dudv = dudv.} \] Теперь можно вычислить двойной интеграл. \[ {\iint\limits_R {\left( {{x^2} + {y^2}} \right)dxdy} } = {\iint\limits_S {\left[ {{{\left( {v - u} \right)}^2} + {v^2}} \right]dudv} } = {\iint\limits_S {\left( {{v^2} - 2uv + {u^2} + {v^2}} \right)dudv} } = {\int\limits_a^{2a} {\left[ {\int\limits_0^a {\left( {2{v^2} - 2uv + {u^2}} \right)du} } \right]dv} } = {\int\limits_a^{2a} {\left[ {\left. {\left( {2{v^2}u - v{u^2} + \frac{{{u^3}}}{3}} \right)} \right|_{u = 0}^a} \right]dv} } = {\int\limits_a^{2a} {\left( {2a{v^2} - {a^2}v + \frac{{{a^3}}}{3}} \right)dv} } = {\left. {\left( {2a \cdot \frac{{{v^3}}}{3} - {a^2} \cdot \frac{{{v^2}}}{2} + \frac{{{a^3}}}{3} \cdot v} \right)} \right|_a^{2a} } = {\left( {\frac{{2a}}{3} \cdot 8{a^3} - \frac{{{a^2}}}{2} \cdot 4{a^2} + \frac{{{a^3}}}{3} \cdot 2a} \right) } - {\left( {\frac{{2a}}{3} \cdot {a^3} - \frac{{{a^2}}}{2} \cdot {a^2} + \frac{{{a^3}}}{3} \cdot a} \right) } = {\frac{{7{a^4}}}{2}.} \]