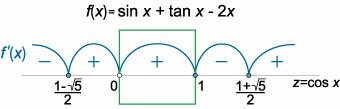Доказательство неравенств

В этом разделе мы рассмотрим, как можно использовать производную для доказательства неравенств. Общий подход состоит в том, чтобы с помощью производной исследовать свойства функций, входящих в неравенство. Наиболее важными являются свойства монотонности и ограниченности функций. Кроме того, для решения неравенств часто применяется теорема Лагранжа. Типичные примеры на эту тему приведены ниже.

   Пример 1

Доказать неравенство \(\sqrt {1 + x} \le 1 + \large\frac{x}{2}\) при \(x > 1\).

Рассмотрим функцию \(f\left( x \right) = \sqrt {1 + x} - \large\frac{x}{2} \normalsize - 1\) и найдем ее производную: \[ {f'\left( x \right) = {\left( {\sqrt {1 + x} - \frac{x}{2} - 1} \right)^\prime } } = {\frac{1}{{2\sqrt {1 + x} }} - \frac{1}{2} } = {\frac{{1 - \sqrt {1 + x} }}{2} \le 0.} \] Учтем, что здесь \(f\left( 0 \right) = 1 - 0 - 1 = 0\). Поэтому \(f\left( x \right) \le 0\) при \(x > 0\). Тогда \[ {\sqrt {1 + x} - \frac{x}{2} - 1 \le 0,}\;\;\;\;\; {\Rightarrow \;\;\sqrt {1 + x} \le 1 + \frac{x}{2}.} \]

   Пример 2

Определить, что больше: \({100^{101}}\) или \({101^{100}}\)?

Рассмотрим функцию \(f\left( x \right) = \large\frac{{\ln x}}{x}\). Вычислим ее производную: \[f'\left( x \right) = {{\left( {\frac{{\ln x}}{x}} \right)^\prime } } = {\frac{{{{\left( {\ln x} \right)}^\prime } \cdot x - \ln x \cdot x'}}{{{x^2}}} } = {\frac{{\frac{1}{x} \cdot x - \ln x}}{{{x^2}}} = \frac{{1 - \ln x}}{{{x^2}}}.} \] Как видно, при условии \(x > e\) производная будет отрицательной. Тогда при \(x > e\) функция \(f(x)\) является убывающей и, следовательно, выполняется соотношение \(\large\frac{{\ln 100}}{{100}} > \frac{{\ln 101}}{{101}}\). Отсюда получаем, что \[101\ln 100 > 100\ln 101,\;\;\;\;\; {\Rightarrow \;\;{100^{101}} > {101^{100}}.} \]

   Пример 3

Доказать, что для любых положительных чисел \(a\) и \(b\) справедливо неравенство \(\large\frac{a}{b} + \frac{b}{a} \normalsize\ge 2\).

Обозначим \(\large\frac{a}{b}\normalsize = x\) и рассмотрим функцию \(f\left( x \right) = x + \large\frac{1}{x}\), учитывая, что \(x > 0\). Определим точки экстремума данной функции: \[f'\left( x \right) = {{\left( {x + \frac{1}{x}} \right)^\prime } } = {1 - \frac{1}{{{x^2}}} = 0,}\;\;\;\;\; {\Rightarrow \;\;{x^2} = 1,}\;\;\;\;\; {\Rightarrow \;\;x = \pm 1.} \] Условию \(x > 0\) удовлетворяет лишь единственная точка \(x = 1\). Поскольку при переходе через эту точку (слева направо) производная меняет знак с минуса на плюс, то точка \(x = 1\) является точкой минимума.

Значение функции в этой точке равно \(f\left( 1 \right) = 1 + \large\frac{1}{1}\normalsize = 2\). Следовательно, \[f\left( x \right) \ge 2,\;\;\;\;\; {\Rightarrow \;\;x + \frac{1}{x} \ge 2,}\;\;\;\;\; {\Rightarrow \;\;\frac{a}{b} + \frac{b}{a} \ge 2.} \]

   Пример 4

Доказать, что при \(x > 0\) справедливо неравенство \(1 + 2\ln x \le {x^2}\).

Введем функцию \(f\left( x \right) = {x^2} - 2\ln x - 1\). Найдем критические точки: \[f'\left( x \right) = {{\left( {{x^2} - 2\ln x - 1} \right)^\prime } } = {2x - \frac{2}{x} = 0,}\;\;\;\;\; {\Rightarrow \;\;\frac{{2{x^2} - 2}}{x} = 0,}\;\;\;\;\; {\Rightarrow \;\;2{x^2} - 2 = 0,}\;\;\;\;\; {\Rightarrow \;\;{x^2} = 1,}\;\;\;\;\; {\Rightarrow \;\;x = \pm 1.} \] Из трех критических точек \(x = -1\), \(x = 0\), \(x = 1\) условию \(x > 0\) удовлетворяет только последняя точка \(x = 1\). Слева от нее производная отрицательна, а справа − положительна. Следовательно, в этой точке функция имеет минимум, равный \[f\left( 1 \right) = 1 - 2\ln 1 - 1 = 0.\] Итак, \(f(x) \ge 0\) при \(x > 0\) (и равна нулю при \(x = 1\)). В таком случае \[{x^2} - 2\ln x - 1 \ge 0,\;\;\;\;\; \Rightarrow \;\;1 + 2\ln x \le {x^2}.\]

   Пример 5

Доказать, что при \(x > 0\) справедливо неравенство \(\ln x \le x - 1\).

Введем функцию \(f\left( x \right) = \ln x - x + 1\). Эта функция определена при \(x > 0\). Ее производная равна \[f'\left( x \right) = {\left( {\ln x - x + 1} \right)^\prime } = \frac{1}{x} - 1.\] При \(0 < x < 1\) производная положительна, а при \(x > 1\) − отрицательна. Следовательно, в точке \(x = 1\) функция \(f(x)\) имеет максимум, равный \[f\left( 1 \right) = \ln 1 - 1 + 1 = 0.\] Таким образом, при \(x > 0\) выполняется неравенство \[f\left( x \right) \le 0,\;\;\;\;\; {\Rightarrow \;\;\ln x - x + 1 \le 0,}\;\;\;\;\; {\Rightarrow \;\;\ln x \le x - 1.} \]

   Пример 6

Показать, что при \(x > 1\) выполняется неравенство \(\sqrt x + \large\frac{1}{{\sqrt x }}\normalsize > 2\).

Рассмотрим функцию \(f\left( x \right) = \sqrt x + \large\frac{1}{{\sqrt x }}\normalsize - 2\). Ее производная имеет вид: \[f'\left( x \right) = {{\left( {\sqrt x + \frac{1}{{\sqrt x }} - 2} \right)^\prime } } = {{\left( {{x^{1/2}} + {x^{ - 1/2}} - 2} \right)^\prime } } = {\frac{1}{2}{x^{ - 1/2}} - \frac{1}{2}{x^{ - 3/2}} = \frac{1}{{2{x^{1/2}}}} - \frac{1}{{2{x^{3/2}}}} } = {\frac{{x - 1}}{{2{x^{3/2}}}} = \frac{{x - 1}}{{2x\sqrt x }}.} \] Как видно, производная положительна при \(x > 1\). Следовательно, функция является возрастающей при \(x > 1\).

Поскольку \(f\left( 1 \right) = \sqrt 1 - \large\frac{1}{{\sqrt 1 }}\normalsize - 2 = 0\), то функция \(f(x)\) положительна при всех \(x > 1\). Таким образом, при \(x > 1\) справедливо следующее неравенство: \[f\left( x \right) > 0,\;\;\;\;\; {\Rightarrow \;\;\sqrt x + \frac{1}{{\sqrt x }} - 2 > 0,}\;\;\;\;\; {\Rightarrow \;\;\sqrt x + \frac{1}{{\sqrt x }} > 2.} \]

   Пример 7

Доказать неравенство \(\large\frac{{b - a}}{b}\normalsize \le \ln \large\frac{b}{a}\normalsize \le \large\frac{{b - a}}{a}\) при условии \(0 < a \le b\).

Рассмотрим логарифмическую функцию \(f\left( x \right) = \ln x\) и применим к ней формулу Лагранжа на отрезке \([a, b]\): \[\frac{{f\left( b \right) - f\left( a \right)}}{{b - a}} = f'\left( \xi \right),\;\;\;\xi \in \left( {a,b} \right).\] Следовательно, \[\frac{{\ln b - \ln a}}{{b - a}} = {\frac{1}{\xi },}\;\;\;\;\; {\Rightarrow \;\;\ln \frac{b}{a} } = {\left( {b - a} \right)\frac{1}{\xi }.} \] Правая часть этого равенства минимальна при \(\xi = b\) и, соответственно, максимальна при \(\xi = a\). Поэтому получаем двойное неравенство, которое требовалось доказать: \[\frac{{b - a}}{b} \le \ln \frac{b}{a} \le \frac{{b - a}}{a}.\]

   Пример 8

Доказать неравенство \(\left| {\sin a - \sin b} \right| \le \left| {a - b} \right|\).

Пусть функция \(f\left( x \right) = \sin x\) задана на отрезке \([a, b]\). Применяя к этой функции теорему Лагранжа, можно записать следующее соотношение: \[\frac{{\sin b - \sin a}}{{b - a}} = \cos \xi ,\] где \(\xi\) − некоторая промежуточная точка, лежащая в интервале \((a, b)\).

Отсюда получаем \[\sin b - \sin a = \left( {b - a} \right)\cos \xi ,\;\;\;\;\; {\Rightarrow \;\;\sin a - \sin b = \left( {a - b} \right)\cos \xi .} \] Перейдем в последнем выражении к модулям: \[\left| {\sin a - \sin b} \right| = \left| {a - b} \right|\left| {\cos \xi } \right|.\] и учтем, что \(\left| {\cos \xi } \right| \le 1\). Следовательно, \[\left| {\sin a - \sin b} \right| \le \left| {a - b} \right|.\]

   Пример 9

Доказать неравенство \(\left| {\arctan a - \arctan b} \right| \le \left| {a - b} \right|\).

Рассмотрим функцию \(f\left( x \right) = \arctan x\) на отрезке \([a, b]\). Применим далее теорему Лагранжа: \[\frac{{f\left( b \right) - f\left( a \right)}}{{b - a}} = f'\left( \xi \right),\] где \(\xi \in \left( {a,b} \right)\). Тогда \[\frac{{\arctan b - \arctan a}}{{b - a}} = \frac{1}{{1 + {\xi ^2}}},\;\;\;\;\; {\Rightarrow \;\;\arctan b - \arctan a = \left( {b - a} \right)\frac{1}{{1 + {\xi ^2}}}.} \] После умножения обеих частей равенства на \(-1\), получаем \[\arctan a - \arctan b = \left( {a - b} \right)\frac{1}{{1 + {\xi ^2}}}.\] Перейдем в данном уравнении к модулям: \[\left| {\arctan a - \arctan b} \right| = \left| {a - b} \right|\left| {\frac{1}{{1 + {\xi ^2}}}} \right|.\] Заметим, что всегда выполняется соотношение \(\large\left| {\frac{1}{{1 + {\xi ^2}}}} \right|\normalsize = \large\frac{1}{{1 + {\xi ^2}}}\normalsize \le 1\). Таким образом, \[\left| {\arctan a - \arctan b} \right| \le \left| {a - b} \right|.\]

   Пример 10

Доказать, что при \(x \ne 0\) выполняется неравенство \({e^x} > 1 + x\).

Рассмотрим функцию \(f\left( x \right) = {e^x} - x - 1\). Исследуем ее на монотонность. Производная записывается в виде \[f'\left( x \right) = {\left( {{e^x} - x - 1} \right)^\prime } = {e^x} - 1.\] При \(x < 0\) производная отрицательна, а при \(x > 0\) − положительна (рис.1). Следовательно, функция \(f(x)\) убывает при \(x < 0\) и возрастает при \(x > 0\). В точке \(x = 0\) она имеет максимум, равный \[f\left( 0 \right) = {e^0} - 0 - 1 = 0.\] Следовательно, функция \(f(x)\) всюду положительна, кроме точки \(x = 0\). В результате получаем \[f\left( x \right) > 0,\;\;\;\;\; {\Rightarrow \;\;{e^x} - x - 1 > 0,}\;\;\;\;\; {\Rightarrow \;\;{e^x} > 1 + x\;\;\left( {x \ne 0} \right).} \]

   Пример 11

Доказать, что в интервале \(\left( {0,\large\frac{\pi }{2}} \right)\) выполняется неравенство \(\sin x + \tan x > 2x\).

Введем функцию \(f\left( x \right) = \sin x + \tan x - 2x\) и исследуем ее на монотонность. Найдем производную: \[f'\left( x \right) = {{\left( {\sin x + \tan x - 2x} \right)^\prime } } = {\cos x + \frac{1}{{{{\cos }^2}x}} - 2.} \] Определим интервалы, в которых производная имеет постоянный знак. Уравнение \(f'\left( x \right) = 0\) можно свести к кубическому: \[f'\left( x \right) = 0,\;\;\;\;\; {\Rightarrow \;\;\cos x + \frac{1}{{{{\cos }^2}x}} - 2 = 0,}\;\;\;\;\; {\Rightarrow \;\;\frac{{{{\cos }^3}x - 2{{\cos }^2}x + 1}}{{{{\cos }^2}x}} = 0,}\;\;\;\;\; {\Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}} {{{\cos }^3}x - 2{{\cos }^2}x + 1 = 0}\\ {\cos x \ne 0} \end{array}} \right..} \] Сделаем замену \(\cos x = z\) и вычислим корни кубического уравнения: \[{z^3} - 2{z^2} + 1 = 0,\;\;\; {\Rightarrow \;\;{z^3} - {z^2} - {z^2} + z - z + 1 = 0,}\;\;\; {\Rightarrow \;\;{z^2}\left( {z - 1} \right) - z\left( {z - 1} \right) - \left( {z - 1} \right) = 0,}\;\;\; {\Rightarrow \;\;\left( {z - 1} \right)\left( {{z^2} - z - 1} \right) = 0,\;\;\;\;\; \Rightarrow \;\;{z_1} = 1.} \] Решая квадратное уравнение \({z^2} - z - 1 = 0\), получаем: \[{z^2} - z - 1 = 0,\;\;\; {\Rightarrow \;\;D = 1 + 4 = 5,}\;\;\; {\Rightarrow \;\;{z_{2,3}} = \frac{{1 \pm \sqrt 5 }}{2} \approx - 0.62;\;1.62} \] Отметим найденные критические точки на оси \(z\) и определим характер изменения знака при переходе через каждую точку (рис.2).

Интервал \(\left( {0,\large\frac{\pi }{2}} \right)\) для переменной \(x\) соответствует интервалу \((0, 1)\) для переменной \(z\). В нем переменная \(z\) положительна, т.е. функция \(f(x)\) в интервале \(\left( {0,\large\frac{\pi }{2}} \right)\) монотонно возрастает.

Поскольку \[f\left( 0 \right) = \sin 0 + \tan 0 - 2 \cdot 0 = 0,\] то, очевидно, в интервале \(\left( {0,\large\frac{\pi }{2}} \right)\) функция \(f(x)\) положительна. Следовательно, \[\sin x + \tan x - 2x > 0,\;\;\; {\Rightarrow \;\;\sin x + \tan x > 2x,\;\;x \in \left( {0,\frac{\pi }{2}} \right).} \]

   Пример 12

Доказать неравенство \(\large\frac{{\tan {x_2}}}{{\tan {x_1}}}\normalsize > \large\frac{{{x_2}}}{{{x_1}}}\) при условии \(0 < {x_1} < {x_2} < \large\frac{\pi }{2}\).

Рассмотрим функцию \(f\left( x \right) = \large\frac{{\tan x}}{x}\). Ее производная имеет такой вид: \[f'\left( x \right) = {\left( {\frac{{\tan x}}{x}} \right)^\prime } = {\frac{{\large\frac{1}{{{{\cos }^2}x}}\normalsize \cdot x - \tan x \cdot 1}}{{{x^2}}} } = {\frac{{\large\frac{x}{{{{\cos }^2}x}}\normalsize - \tan x}}{{{x^2}}} } = {\frac{{x - \sin x\cos x}}{{{x^2}{{\cos }^2}x}}.} \] В нашем случае знаменатель в последнем выражении всегда положителен. Исследуем знак числителя. Для этого введем еще одну функцию \(g\left( x \right) = x - \sin x\cos x = x - \frac{1}{2}\sin 2x\;\) и исследуем ее также с помощью производной. В результате имеем \[g'\left( x \right) = {\left( {x - \frac{1}{2}\sin 2x} \right)^\prime } ={ 1 - \cos 2x \ge 0,} \] Учитывая, что \(g\left( 0 \right) = 0\), приходим к выводу, что числитель в выражении для производной \(f'(x)\) также положителен.

Таким образом, производная \(f'(x)\) положительна в интервале \(\left( {0,\large\frac{\pi }{2}} \right)\) и, следовательно, функция \(f(x)\) возрастает в этом интервале. Отсюда для \(0 < {x_1} < {x_2} < \large\frac{\pi }{2}\) следует соотношение \[\frac{{\tan {x_2}}}{{{x_2}}} > \frac{{\tan {x_1}}}{{{x_1}}},\;\;\;\;\; {\Rightarrow \;\;\frac{{\tan {x_2}}}{{\tan {x_1}}} > \frac{{{x_2}}}{{{x_1}}}.} \]