Дифференциал функции

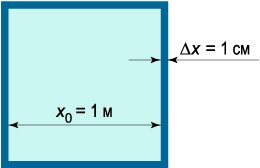
Рассмотрим функцию \(y = f\left( x \right),\) которая является непрерывной в интервале \(\left[ {a,b} \right].\) Предположим, что в некоторой точке \({x_0} \in \left[ {a,b} \right]\) независимая переменная получает приращение \(\Delta x.\) Приращение функции \(\Delta y,\) соответствующее такому изменению аргумента \(\Delta x,\) выражается формулой \[\Delta y = \Delta f\left( {{x_0}} \right) = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right).\] Для любой дифференцируемой функции приращение \(\Delta y\) можно представить в виде суммы двух слагаемых: \[\Delta y = A\Delta x + \omicron\left( {\Delta x} \right),\] где первый член (т.н. главная часть приращения) линейно зависит от приращения \(\Delta x,\) а второй член имеет более высокий порядок малости относительно \(\Delta x.\) Выражение \(A\Delta x\) называется дифференциалом функции и обозначается символом \(dy\) или \(df\left( {{x_0}} \right).\) Рассмотрим эту идею разбиения приращения функции \(\Delta y\) на две части на простом примере. Пусть задан квадрат со стороной \({x_0} = 1 \,\text{м}\,\) (рисунок \(1\)). Его площадь, очевидно, равна \[{S_0} = x_0^2 = 1 \,\text{м}^2.\] Если сторону квадрата увеличить на \(\Delta x = 1\,\text{см},\) то точное значение площади увеличенного квадрата будет составлять \[S = {x^2} = {\left( {{x_0} + \Delta x} \right)^2} = 1,{01^2} = 1,0201 \,\text{м}^2,\] т.е. приращение площади \(\Delta S\) равно \[ {\Delta S = S - {S_0} = 1,0201 - 1 = 0,0201\,\text{м}^2 } = {201\,\text{см}^2.} \] Представим теперь это приращение \(\Delta S\) в таком виде: \[\require{cancel} {\Delta S = S - {S_0} = {\left( {{x_0} + \Delta x} \right)^2} - x_0^2 } = {\cancel{x_0^2} + 2{x_0}\Delta x + {\left( {\Delta x} \right)^2} - \cancel{x_0^2} } = {2{x_0}\Delta x + {\left( {\Delta x} \right)^2} } = {A\Delta x + \omicron\left( {\Delta x} \right) } = {dy + o\left( {\Delta x} \right).} \] Итак, приращение функции \(\Delta S\) состоит из главной части (дифференциала функции), которая пропорциональна \(\Delta x\) и равна \[dy = A\Delta x = 2{x_0}\Delta x = 2 \cdot 1 \cdot 0,01 = 0,02 \,\text{м}^2 = 200\,\text{см}^2,\] и члена более высокого порядка малости, в свою очередь, равного \[\omicron\left( {\Delta x} \right) = {\left( {\Delta x} \right)^2} = {0,01^2} = 0,0001\,\text{м}^2 = 1\,\text{см}^2.\] В сумме оба этих члена составляют полное приращение площади квадрата, равное \(200 + 1 = 201\,\text{см}^2.\)

Заметим, что в данном примере коэффициент \(A\) равен значению производной функции \(S\) в точке \({x_0}:\) \[A = 2{x_0}.\] Оказывается, что для любой дифференцируемой функции справедлива следующая теорема:

Коэффициент \(A\) главной части приращения функции в точке \({x_0}\) равен значению производной \(f'\left( {{x_0}} \right)\) в этой точке, т.е. приращение \(\Delta y\) выражается формулой \[ {\Delta y = A\Delta x + \omicron\left( {\Delta x} \right) } = {f'\left( {{x_0}} \right)\Delta x + \omicron\left( {\Delta x} \right).} \] Разделив обе части этого равенства на \(\Delta x \ne 0,\) имеем \[ {\frac{{\Delta y}}{{\Delta x}} = A + \frac{{\omicron\left( {\Delta x} \right)}}{{\Delta x}} } = {f'\left( {{x_0}} \right) + \frac{{\omicron\left( {\Delta x} \right)}}{{\Delta x}}.} \] В пределе при \(\Delta x \to 0\) получаем значение производной в точке \({x_0}:\) \[ {y'\left( {{x_0}} \right) = \lim\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} } = {A = f'\left( {{x_0}} \right).} \] Здесь мы учли, что для малой величины \(\omicron\left( {\Delta x} \right)\) более высокого порядка малости, чем \(\Delta x,\) предел равен \[\lim\limits_{\Delta x \to 0} \frac{{\omicron\left( {\Delta x} \right)}}{{\Delta x}} = 0.\] Если считать, что дифференциал независимой переменной \(dx\) равен ее приращению \(\Delta x:\) \[dx = \Delta x,\] то из соотношения \[dy = A\Delta x = y'dx\] следует, что \[y' = \frac{{dy}}{{dx}},\] т.е. производную функции можно представить как отношение двух дифференциалов. На рисунке \(2\) схематически показана разбивка приращения функции \(\Delta y\) на главную часть \(A\Delta x\) (дифференциал функции) и член высшего порядка малости \(\omicron\left( {\Delta x} \right)\).

Касательная \(MN\), проведенная к кривой функции \(y = f\left( x \right)\) в точке \(M\), как известно, имеет угол наклона \(\alpha\), тангенс которого равен производной: \[\tan \alpha = f'\left( {{x_0}} \right).\] При изменении аргумента на \(\Delta x\) касательная получает приращение \(A\Delta x.\) Это линейное приращение, образованное касательной, как раз и является дифференциалом функции. Остальная часть полного приращения \(\Delta y\) (отрезок \(N{M_1}\)) соответствует "нелинейной" добавке с более высоким порядком малости относительно \(\Delta x\). Пусть \(u\) и \(v\) − функции переменной \(x\). Дифференциал обладает следующими свойствами:

1. Постоянный коэффициент можно выносить за знак дифференциала:
   \(d\left( {Cu} \right) = Cdu\), где \(C\) − постоянное число.
2. Дифференциал суммы (разности) функций:
   \(d\left( {u \pm v} \right) = du \pm dv.\)
3. Дифференциал постоянной величины равен нулю:
   \(d\left( C \right) = 0.\)
4. Дифференциал независимой переменной \(x\) равен ее приращению:
   \(dx = \Delta x.\)
5. Дифференциал линейной функции равен ее приращению:
   \(d\left( {ax + b} \right) = \Delta \left( {ax + b} \right) = a\Delta x.\)
6. Дифференциал произведения двух функций:
   \(d\left( {uv} \right) = du \cdot v + u \cdot dv.\)
7. Дифференциал частного двух функций:
   \(d\left( {\large\frac{u}{v}\normalsize} \right) = \large\frac{{du \cdot v - u \cdot dv}}{{{v^2}}}\normalsize.\)
8. Дифференциал функции равен произведению производной на дифференциал аргумента:
   \(dy = df\left( x \right) = f'\left( x \right)dx.\)

Как видно, дифференциал функции \(dy\) отличается от производной лишь множителем \(dx\). Например, \[ {d\left( {{x^n}} \right) = n{x^{n - 1}}dx,}\;\; {d\left( {\ln x} \right) = \frac{{dx}}{x},}\;\; {d\left( {\sin x} \right) = \cos x dx} \] и так далее. Рассмотрим композицию двух функций \(y = f\left( u \right)\) и \(u = g\left( x \right),\) т.е. сложную функцию \(y = f\left( {g\left( x \right)} \right).\) Ее производная определяется выражением \[{y'_x} = {y'_u} \cdot {u'_x},\] где нижний индекс обозначает переменную, по которой производится дифференцирование.

Дифференциал "внешней" функции \(y = f\left( u \right)\) записывается в виде \[dy = {y'_u}\,du.\] Дифференциал "внутренней" функции \(u = g\left( x \right)\) можно представить аналогичным образом: \[du = {u'_x}\,dx.\] Если подставить \(du\) в предыдущую формулу, то получим \[dy = {y'_u}\,du = {y'_u}{u'_x}\,dx.\] Поскольку \({y'_x} = {y'_u} \cdot {u'_x},\) то \[dy = {y'_x}\,dx.\] Видно, что в случае сложной функции мы получили такое же по форме выражение для дифференциала функции, как и в случае "простой" функции. Это свойство называется инвариантностью формы дифференциала.

   Пример 1

Найти дифференциал функции \(y = \sin x - x\cos x.\) Найдем производную заданной функции: \[\require{cancel} {y' = {\left( {\sin x - x\cos x} \right)^\prime } } = {\cos x - \left( {x'\cos x + x{{\left( {\cos x} \right)}^\prime }} \right) } = {\cos x - \left( {\cos x + x\left( { - \sin x} \right)} \right) } = {\cancel{\cos x} - \cancel{\cos x} + x\sin x = x\sin x.} \] Дифференциал имеет следующий вид: \[dy = y'dx = x\sin x\,dx.\]

   Пример 2

Найти дифференциал функции \(y = \cot \large\frac{{\pi x}}{4}\normalsize\) в точке \(x = 1\). Находим производную и вычисляем ее значение в заданной точке: \[ {y' = {\left( {\cot \frac{{\pi x}}{4}} \right)^\prime } } = { - \frac{1}{{{{\sin }^2}\left( {\frac{{\pi x}}{4}} \right)}} \cdot \frac{\pi }{4} } = { - \frac{\pi }{{4{{\sin }^2}\left( {\frac{{\pi x}}{4}} \right)}},}\;\; {\Rightarrow y'\left( 1 \right) = - \frac{\pi }{{4{{\sin }^2}\left( {\frac{\pi }{4}} \right)}} } = { - \frac{\pi }{{4{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}}} = - \frac{\pi }{2}.} \] Тогда \[dy = y'dx = - \frac{\pi }{2}dx.\]

   Пример 3

Найти дифференциал функции \(y = 2{x^2} + 3x + 1\) в точке \(x = 1\) при \(dx = 0,1.\) \[ {dy = f'\left( x \right)dx = {\left( {2{x^2} + 3x + 1} \right)^\prime }dx } = {\left( {4x + 3} \right)dx.} \] Подставляя заданные значения, вычисляем дифференциал: \[dy = \left( {4 \cdot 1 + 3} \right) \cdot 0,1 = 0,7.\]

   Пример 4

Вычислить приращение и дифференциал функции \(y = {x^2} - x + 1\) в точке \(x = 2\) при \(dx = 1.\) Определим приращение функции по формуле \[\Delta y = f\left( {x + \Delta x} \right) - f\left( x \right).\] Поскольку здесь \(x + \Delta x = 2 + 1 = 3,\) то получаем \[ {\Delta y = f\left( 3 \right) - f\left( 2 \right) } = {\left( {{3^2} - 3 + 1} \right) - \left( {{2^2} - 2 + 1} \right) } = {7 - 3 = 4.} \] Дифференциал (или линейная часть приращения) при этом составляет: \[ {dy = f'\left( x \right)\Delta x = {\left( {{x^2} - x + 1} \right)^\prime }\Delta x } = {\left( {2x - 1} \right)\Delta x } = {\left( {2 \cdot 2 - 1} \right) \cdot 1 = 3.} \]

   Пример 5

Найти дифференциал функции \(y = {x^x}{e^{2x}}\) в точке \(x = 1\). \[ {y' = {\left( {{x^x}{e^{2x}}} \right)^\prime } } = {{\left( {{x^x}} \right)^\prime }{e^{2x}} + {x^x}{\left( {{e^{2x}}} \right)^\prime }.} \] Производная функции \({x^x}\) равна \[ {{\left( {{x^x}} \right)^\prime } = {\left( {{e^{\ln x \cdot x}}} \right)^\prime } } = {{\left( {{e^{x\ln x}}} \right)^\prime } } = {{e^{x\ln x}}{\left( {x\ln x} \right)^\prime } } = {{x^x}\left( {1 \cdot \ln x + x \cdot \frac{1}{x}} \right) } = {{x^x}\left( {\ln x + 1} \right).} \] Следовательно, производная исходной функции имеет вид: \[ {y' = {x^x}\left( {\ln x + 1} \right){e^{2x}} + {x^x} \cdot 2{e^{2x}} } = {{x^x}{e^{2x}}\left( {\ln x + 1 + 2} \right) } = {{x^x}{e^{2x}}\left( {\ln x + 3} \right).} \] При \(x = 1\), соответственно, получаем: \[y'\left( 1 \right) = {1^1} \cdot {e^2} \cdot \left( {\ln 1 + 3} \right) = 3{e^2}.\] Тогда дифференциал функции в данной точке записывается как \[dy = y'dx = 3{e^2}dx.\]

   Пример 6

Найти дифференциал функции \(y = x\sin \large\frac{{\pi x}}{2}\normalsize\) в точке \(x = \large\frac{1}{2}\normalsize\) при \(dx = 0,01.\) \[ {dy = f'\left( y \right)dx = {\left( {x\sin \frac{{\pi x}}{2}} \right)^\prime }dx } = {\left( {1 \cdot \sin \frac{{\pi x}}{2} + x \cdot \cos \frac{{\pi x}}{2} \cdot \frac{\pi }{2}} \right)dx } = {\left( {\sin \frac{{\pi x}}{2} + \frac{{\pi x}}{2}\cos \frac{{\pi x}}{2}} \right)dx.} \] Подставляем значения \(x\) и \(dx\) и вычисляем дифференциал \(dy:\) \[ {dy = \left( {\sin \frac{{\pi \cdot \frac{1}{2}}}{2} + \frac{{\pi \cdot \frac{1}{2}}}{2}\cos \frac{{\pi \cdot \frac{1}{2}}}{2}} \right) \cdot 0,01 } = {\left( {\sin \frac{\pi }{4} + \frac{\pi }{4}\cos \frac{\pi }{4}} \right) \cdot 0,01 } = {\left( {\frac{{\sqrt 2 }}{2} + \frac{\pi }{4}\frac{{\sqrt 2 }}{2}} \right) \cdot 0,01 } = {\frac{{\sqrt 2 }}{{200}}\left( {1 + \frac{\pi }{4}} \right) \approx 0,0126.} \]

   Пример 7

Вычислить приращение и дифференциал функции \(y = \large\frac{{x + 2}}{{x + 1}}\normalsize\) в точке \(x = 0\) при \(\Delta x = 0,1.\) Найдем сначала приращение функции: \[ {\Delta y = f\left( {x + \Delta x} \right) - f\left( x \right) } = {\frac{{x + \Delta x + 2}}{{x + \Delta x + 1}} - \frac{{x + 2}}{{x + 1}} } = {\frac{{0,1 + 2}}{{0,1 + 1}} - \frac{2}{1} } = {1,9091 - 2 \approx - 0,0909.} \] При тех же значениях \(x\) и \(\Delta x\) дифференциал функции равен \[ {dy = f'\left( x \right)\Delta x = {\left( {\frac{{x + 2}}{{x + 1}}} \right)^\prime }\Delta x } = {\frac{{{{\left( {x + 2} \right)}^\prime }\left( {x + 1} \right) - \left( {x + 2} \right){{\left( {x + 1} \right)}^\prime }}}{{{{\left( {x + 1} \right)}^2}}}\Delta x } = {\frac{{\cancel{x} + 1 - \cancel{x} - 2}}{{{{\left( {x + 1} \right)}^2}}}\Delta x } = { - \frac{1}{{{{\left( {x + 1} \right)}^2}}}\Delta x } = { - \frac{1}{{{1^2}}} \cdot 0,1 = - 0,1.} \]

   Пример 8

Найти дифференциал функции \(y = \large\frac{1}{{\sqrt {{u^2} + {v^2}} }}\normalsize,\) где \(u\) и \(v\) − дифференцируемые функции переменной \(x\). Используя правила дифференцирования, получаем: \[ {dy = d\left( {\frac{1}{{\sqrt {{u^2} + {v^2}} }}} \right) } = {d\left[ {{{\left( {{u^2} + {v^2}} \right)}^{ - \large\frac{1}{2}\normalsize}}} \right] } = { - \frac{1}{2}{\left( {{u^2} + {v^2}} \right)^{ - \large\frac{3}{2}\normalsize}}d\left( {{u^2} + {v^2}} \right) } = { - \frac{1}{{2{{\left( {{u^2} + {v^2}} \right)}^{\large\frac{3}{2}\normalsize}}}}\left[ {d\left( {{u^2}} \right) + d\left( {{v^2}} \right)} \right] } = { - \frac{{2udu + 2vdv}}{{2\sqrt {{{\left( {{u^2} + {v^2}} \right)}^3}} }} } = { - \frac{{udu + vdv}}{{\sqrt {{{\left( {{u^2} + {v^2}} \right)}^3}} }}.} \]

   Пример 9

Найти дифференциал функции \(y = \arcsin \large\frac{u}{v}\normalsize,\) где \(u\) и \(v\) − дифференцируемые функции от \(x\). \[ {dy = d\left( {\arcsin \frac{u}{v}} \right) } = {\frac{1}{{\sqrt {1 - {{\left( {\frac{u}{v}} \right)}^2}} }}d\left( {\frac{u}{v}} \right) } = {\frac{1}{{\sqrt {1 - {{\left( {\frac{u}{v}} \right)}^2}} }} \cdot \frac{{vdu - udv}}{{{v^2}}} } = {\frac{{\left| v \right|}}{{\sqrt {{v^2} - {u^2}} }} \cdot \frac{{vdu - udv}}{{{{\left| v \right|}^2}}} } = {\frac{{vdu - udv}}{{\left| v \right|\sqrt {{v^2} - {u^2}} }},} \] где \({v^2} > {u^2},\;v \ne 0.\)

   Пример 10

Функция \(y\left( x \right)\) задана неявным уравнением \({y^3} - 3xy + {x^3} = 3.\) Найти ее дифференциал в точке \(\left( {2,1} \right).\) Определим производную неявной функции. Дифференцируя обе части по \(x\), получаем: \[ {{\left( {{y^3} - 3xy + {x^3}} \right)^\prime } = {\left( 3 \right)^\prime },}\;\; {\Rightarrow 3{y^2}y' - \left( {3y + 3xy'} \right) + 3{x^2} = 0,}\;\; {\Rightarrow 3{y^2}y' - 3y - 3xy' + 3{x^2} = 0,}\;\; {\Rightarrow \left( {{y^2} - x} \right)y' = y - {x^2},}\;\; {\Rightarrow y' = \frac{{y - {x^2}}}{{{y^2} - x}}.} \] В точке \(\left( {2,1} \right)\) производная \(y'\) имеет значение \[y'\left( {2,1} \right) = \frac{{1 - {2^2}}}{{{1^2} - 2}} = 3.\] Соответственно, дифференциал в этой точке записывается как \[dy = y'dx = 3dx.\]

   Пример 11

Функция \(y\left( x \right)\) задана неявным уравнением \({x^2} - \sqrt y \,\ln y = 1.\) Найти ее дифференциал в точке \(\left( {1,1} \right).\) Дифференцируем обе части уравнения по \(x\) и находим производную \(y':\) \[ {{\left( {{x^2} - \sqrt y \ln y} \right)^\prime } = 1',}\;\; {\Rightarrow 2x - \left( {\frac{1}{{2\sqrt y }} \cdot y' \cdot \ln y + \sqrt y \cdot \frac{1}{y} \cdot y'} \right) = 0,}\;\; {\Rightarrow 2x - y'\left( {\frac{{\ln y}}{{2\sqrt y }} + \frac{1}{{\sqrt y }}} \right) = 0,}\;\; {\Rightarrow 4x\sqrt y - y'\left( {\ln y + 2} \right) = 0,}\;\; {\Rightarrow y' = \frac{{4x\sqrt y }}{{\ln y + 2}}.} \] Вычислим значение производной в заданной точке \(\left( {1,1} \right):\) \[y'\left( {1,1} \right) = \frac{{4 \cdot 1 \cdot \sqrt 1 }}{{\ln 1 + 2}} = 2.\] Дифференциал функции в этой точке равен \[dy = y'dx = 2dx.\]

   Пример 12

Найти дифференциал функции \(y = \arctan \sqrt {\large\frac{{1 - x}}{{1 + x}}\normalsize} .\) Поскольку дифференциал функции выражается формулой \[dy = y'\left( x \right)dx,\] то для его нахождения достаточно вычислить производную \(y'\left( x \right)\). Дифференцируя как сложную функцию, получаем: \[ {y'\left( x \right) = {\left( {\arctan \sqrt {\frac{{1 - x}}{{1 + x}}} } \right)^\prime } } = {\frac{1}{{1 + {{\left( {\sqrt {\frac{{1 - x}}{{1 + x}}} } \right)}^2}}} \cdot {\left( {\sqrt {\frac{{1 - x}}{{1 + x}}} } \right)^\prime } } = {\frac{1}{{1 + \frac{{1 - x}}{{1 + x}}}} \cdot \frac{1}{{2\sqrt {\frac{{1 - x}}{{1 + x}}} }} \cdot {\left( {\frac{{1 - x}}{{1 + x}}} \right)^\prime } } = {\frac{1}{{\frac{{1 + \cancel{x} + 1 - \cancel{x}}}{{1 + x}}}} \cdot \frac{1}{2}\sqrt {\frac{{1 + x}}{{1 - x}}} \cdot \frac{{{{\left( {1 - x} \right)}^\prime }\left( {1 + x} \right) - \left( {1 - x} \right){{\left( {1 + x} \right)}^\prime }}}{{{{\left( {1 + x} \right)}^2}}} } = {\frac{{1 + x}}{2} \cdot \frac{1}{2}\sqrt {\frac{{1 + x}}{{1 - x}}} \cdot \frac{{\left( { - 1} \right) \cdot \left( {1 + x} \right) - \left( {1 - x} \right) \cdot 1}}{{{{\left( {1 + x} \right)}^2}}} } = {\frac{{\left( {1 + x} \right)\sqrt {1 + x} \left( { - 1 - \cancel{x} - 1 + \cancel{x}} \right)}}{{4\sqrt {1 - x} {{\left( {1 + x} \right)}^2}}} } = { - \frac{{\sqrt {1 + x} }}{{2\sqrt {1 - x} \left( {1 + x} \right)}} } = { - \frac{1}{{2\sqrt {\left( {1 - x} \right)\left( {1 + x} \right)} }} } = { - \frac{1}{{2\sqrt {1 - {x^2}} }},} \] где \( - 1 < x < 1.\) Соответственно, дифференциал функции записывается в виде \[dy = - \frac{{dx}}{{2\sqrt {1 - {x^2}} }}.\]

   Пример 13

Функция \(y\left( x \right)\) задана параметрическими уравнениями \[ \left\{ \begin{aligned} x &= t^2 + t + 1 \\ y &= t^3 - 2t \end{aligned} \right.. \] Найти дифференциал функции в точке \(\left( {3, - 1} \right).\) Из уравнения \(3 = {t^2} + t + 1\) определяем соответствующее значение параметра \(t:\) \[ {{t^2} + t - 2 = 0,}\;\; {\Rightarrow D = 9,}\;\; {\Rightarrow {t_{1,2}} = \frac{{ - 1 \pm 3}}{2} = 1, - 2.} \] Проверим, что условию \(y = -1\) удовлетворяет значение \(t = 1.\)

Найдем производную \({y'_x}\) параметрически заданной функции: \[ {{y'_x} = \frac{{{y'_t}}}{{{x'_t}}} } = {\frac{{{{\left( {{t^3} - 2t} \right)}^\prime }}}{{{{\left( {{t^2} + t + 1} \right)}^\prime }}} } = {\frac{{3{t^2} - 2}}{{2t + 1}}.} \] При \(t = 1\) производная имеет следующее значение: \[ {{y'_x}\left( {t = 1} \right) } = {\frac{{3 \cdot {1^2} - 2}}{{2 \cdot 1 + 1}} = \frac{1}{3}.} \] Таким образом, дифференциал функции в точке \(\left( {3, - 1} \right)\) выражается формулой \[dy = {y'_x}\,dx = \frac{{dx}}{3}.\]

   Пример 14

Функция \(y\left( x \right)\) задана параметрическими уравнениями \[ \left\{ \begin{aligned} x &= \left( {t + 2} \right){e^t} \\ y &= {e^{t + 1}} \end{aligned} \right.. \] Найти дифференциал функции в точке \(\left( {2, e} \right).\) Сначала определим значение параметра \(t\), которое соответствует точке \(\left( {2, e} \right).\) Из второго уравнения находим: \[ {e = {e^{t + 1}},}\;\; {\Rightarrow t + 1 = 1,}\;\; {\Rightarrow t = 0.} \] Проверим значение \(x\) при \(t = 0:\) \[x = \left( {0 + 2} \right){e^0} = 2.\] Найдем производную параметрически заданной функции: \[ {{y'_x} = \frac{{{y'_t}}}{{{x'_t}}} } = {\frac{{{{\left( {{e^{t + 1}}} \right)}^\prime }}}{{{{\left( {\left( {t + 2} \right){e^t}} \right)}^\prime }}} } = {\frac{{{e^{t + 1}}}}{{1 \cdot {e^t} + \left( {t + 2} \right){e^t}}} } = {\frac{{\cancel{e^t}e}}{{\cancel{e^t}\left( {1 + t + 2} \right)}} } = {\frac{e}{{t + 3}}.} \] При \(t = 0\) производная, соответственно, равна \[{y'_x}\left( {t = 0} \right) = \frac{e}{3}.\] Следовательно, дифференциал функции в точке \(\left( {2, e} \right)\) имеет вид: \[dy = {y'_x}\,dx = \frac{{e\,dx}}{3}.\]

   Пример 15

Дана сложная функция \(y = \ln x,\;u = \cos x.\) Выразить дифференциал функции \(y\) в инвариантной форме. Запишем дифференциал "внешней" функции: \[ {dy = {y'_u}\,du = {\left( {\ln u} \right)^\prime }du } = {\frac{1}{u}du.} \] Аналогично найдем дифференциал "внутренней" функции: \[ {du = {u'_x}\,dx = {\left( {\cos x} \right)^\prime }dx } = { - \sin x\,dx.} \] Подставляя выражение для \(du\) в предыдущую формулу, получим дифференциал \(dy\) в инвариантной форме: \[ {dy = \frac{1}{u}du = \frac{1}{u}\left( { - \sin x} \right)dx } = { - \frac{{\sin x}}{{\cos x}}dx } = { - \tan x\,dx.} \]