Динамика народонаселения

Рост населения представляет собой динамический процесс, который можно эффективно описать с помощью дифференциальных уравнений. Ниже мы рассмотрим несколько моделей роста, предложенных экономистами и физиками. Простейшая модель роста народонаселения была предложена еще в \(1798\) году британским ученым Томасом Робертом Мальтусом. Эта модель отражает экспоненциальный рост населения и описывается дифференциальным уравнением \[\frac{{dN}}{{dt}} = aN,\] где \(a\) − постоянная роста (мальтузианский параметр). Решением данного уравнения является экспоненциальная функция \[N\left( t \right) = {N_0}{e^{at}},\] где \({N_0}\) соответствует первоначальному размеру популяции.

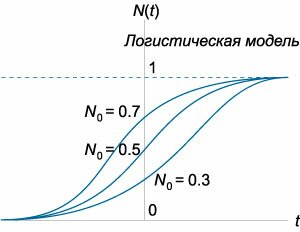
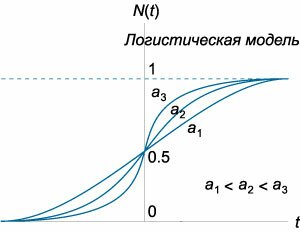
Данная простая модель корректно описывает начальную фазу роста. Однако точность экспоненциальной модели снижается по мере роста населения вследствие насыщения и других нелинейных эффектов (рисунок \(1\)). Данный класс моделей народонаселения был предложен французским математиком Пьером Франсуа Фергельстом в \(1838\) году. Эта модель также называется логистической моделью и записывается в виде следующего дифференциального уравнения: \[\frac{{dN}}{{dt}} = aN\left( {1 - \frac{N}{M}} \right),\] где \(M\) обозначает максимальный размер популяции. Правую часть уравнения можно записать в виде: \[aN - \frac{{a{N^2}}}{M},\] где первое слагаемое соответствует росту популяции, а второе слагаемое ограничивает этот рост из-за отсутствия ресурсов или по другим причинам (рисунки \(2,3\)). Логистическая дифференциальная модель имеет точное решение, которое выводится ниже. \[ {\frac{{dN}}{{dt}} = aN\left( {1 - \frac{N}{M}} \right),}\;\; {\Rightarrow \int {\frac{{dN}}{{N\left( {1 - \frac{N}{M}} \right)}}} = \int {adt} .} \] Подынтегральное выражение в левом интеграле можно разложить на более простые дроби с помощью метода неопределенных коэффициентов: \[ {\frac{1}{{N\left( {1 - \frac{N}{M}} \right)}} = \frac{A}{N} + \frac{B}{{1 - \frac{N}{M}}},}\;\; {\Rightarrow \frac{1}{{N\left( {1 - \frac{N}{M}} \right)}} = \frac{{A\left( {1 - \frac{N}{M}} \right) + BN}}{{N\left( {1 - \frac{N}{M}} \right)}},}\;\; {\Rightarrow 1 \equiv A - A\frac{N}{M} + BN,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {A = 1}\\ {B = \frac{1}{M}} \end{array}} \right..} \] Тогда интеграл в левой части принимает вид: \[ {\int {\frac{{dN}}{{N\left( {1 - \frac{N}{M}} \right)}}} } = {\int {\left( {\frac{1}{N} + \frac{{\frac{1}{M}}}{{1 - \frac{N}{M}}}} \right)dN} } = {\int {\frac{{dN}}{N}} + \int {\frac{{d\left( {\frac{N}{M}} \right)}}{{1 - \frac{N}{M}}}} } = {\ln \left| N \right| - \ln \left| {1 - \frac{N}{M}} \right| } = {\ln \left| {\frac{N}{{1 - \frac{N}{M}}}} \right| } = {\ln \frac{N}{{1 - \frac{N}{M}}}.} \] Таким образом, общее решение логистического дифференциального уравнения записывается в виде: \[ {\ln \frac{N}{{1 - \frac{N}{M}}} = at + \ln C,}\;\; {\Rightarrow \ln \frac{N}{{1 - \frac{N}{M}}} = \ln {e^{at}} + \ln C,}\;\; {\Rightarrow \ln \frac{N}{{1 - \frac{N}{M}}} = \ln C{e^{at}},}\;\; {\Rightarrow \frac{N}{{1 - \frac{N}{M}}} = C{e^{at}}.} \] Последнее алгебраическое уравнение можно разрешить относительно \(N:\) \[ {N = C{e^{at}} - \frac{N}{M}C{e^{at}},}\;\; {\Rightarrow N\left( {1 + \frac{1}{M}C{e^{at}}} \right) = C{e^{at}},}\;\; {\Rightarrow N = \frac{{C{e^{at}}}}{{1 + \frac{1}{M}C{e^{at}}}} = \frac{{CM{e^{at}}}}{{M + C{e^{at}}}}.} \] Постоянная \(C\) определяется из начального условия \(N\left( {t = 0} \right) = {N_0},\) так что \[ {{N_0} = \frac{{CM \cdot 1}}{{M + C}},}\;\; {\Rightarrow CM = {N_0}M + C{N_0},}\;\; {\Rightarrow C = \frac{{{N_0}M}}{{M - {N_0}}}.} \] Подставляя это значение \(C\) в общее решение, получаем: \[ {N\left( t \right) = \frac{{\frac{{{N_0}{M^2}{e^{at}}}}{{M - {N_0}}}}}{{M + \frac{{{N_0}M{e^{at}}}}{{M - {N_0}}}}} } = {\frac{{{N_0}{M^2}{e^{at}}}}{{{M^2} - {N_0}M + {N_0}M{e^{at}}}} } = {\frac{{{N_0}M{e^{at}}}}{{M - {N_0} + {N_0}{e^{at}}}} } = {\frac{{{N_0}M}}{{{N_0} + \left( {M - {N_0}} \right){e^{ - at}}}}.} \] График логистической кривой выглядит очень красиво. Рисунок \(2\) показывает несколько таких кривых при разных значениях \({N_0},\) а рисунок \(3\) показывает как форма логистической кривой зависит от постоянной роста \(a.\)

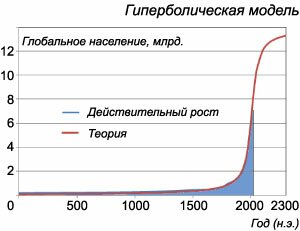
Мы видим, что семейство логистических кривых на отрезке \(t > 0\) может описывать нелинейный рост населения с учетом эффекта насыщения. Рассмотренные выше модели полезны при анализе демографических процессов в масштабе столетий. Если же рассмотреть рост народонаселения в течение нескольких тысяч лет (рисунок \(4\)), то хорошо видно, что основной взрывной рост населения Земли от \(2\) до \(7\) миллиардов человек происходил в последние \(50\) лет. Такой тип зависимости напоминает гиперболическую кривую. Простая гиперболическая модель роста, предложенная несколькими исследователями [Форстер \(\left( {1960} \right),\) Хостер \(\left( {1975} \right),\) Шкловский \(\left( {1980} \right)\)], описывается выражением вида \[N\left( t \right) = \frac{C}{{{T_1} - t}} = \frac{{200}}{{2025 - t}}\,\left( \text{млрд.} \right)\] Из последней формулы следует, что население Земли стремится к бесконечности при приближении к \(2025\) году.

В действительности, реальная динамика населения демонстрирует так называемый демографический переход, который следует за фазой взрывного роста. Это новое состояние характеризуется снижающейся рождаемостью и смертностью. Такой переход уже произошел во многих развитых странах. В результате демографического перехода рост населения прекращается и население может даже убывать. Глобальное население Земли вступило в фазу демографического перехода в начале \(21\) века.

Оказывается, что такая сложная динамика народонаселения может также хорошо описываться с помощью дифференциальных уравнений! Модель данного типа была недавно (\(1997\) г.) разработана российским физиком Сергеем Капицей. С.Капица предложил описывать взрывной рост следующим уравнением: \[\frac{{dN}}{{dt}} = \frac{C}{{{{\left( {{T_0} - t} \right)}^2} + {\tau ^2}}},\] где \({{T_0}}, C\) и \(\tau\) − некоторые параметры аппроксимации. Это дифференциальное уравнение имеет точное решение в виде функции \[N\left( t \right) = \frac{C}{\tau }\text{arccot}\, \frac{{{T_0} - t}}{\tau }.\] Указанная функция замечательно описывает взрывной рост глобального населения при следующих значениях параметров: \(C = 1.86 \times {10^{11}},\) \({T_0} = 2007,\) \(\tau = 42.\) Кроме того, модель учитывает фазу демографического перехода, когда население достигает насыщения (см. рисунок \(4\) выше). Согласно данной модели, население Земли достигнет максимального значения примерно \(12\) миллиардов в \(2200-2300\) г.