|
|
|
|
Геометрические задачи на оптимизацию
|
|
|
В геометрии существует множество задач, в которых требуется найти наибольшее или наименьшее значение функции. В качестве функции могут рассматриваться периметр или площадь фигуры или, например, объем тела, а аргументом функции служит какой-либо параметр фигуры или тела − длина стороны, угол между сторонами и т.п. После того, как функция составлена, ее необходимо исследовать с помощью производной на экстремальное значение. При этом следует учитывать, что обычно в таких примерах функция существует на конечном промежутке, который определяется геометрией системы и условием задачи.
|
|
Пример 1
|
|
На координатной плоскости в первой четверти задана точка \(A\left( {a,b} \right).\) Провести через эту точку прямую, отсекающую треугольник наименьшей площади, ограниченный данной прямой и осями координат (рисунок \(1\)).
Решение.
Рассмотрим треугольники \(OBC\) и \(MBA.\) Эти треугольники подобны. Следовательно, справедливо соотношение \[\frac{{OC}}{{MA}} = \frac{{OB}}{{MB}}\;\;\text{или}\;\;\frac{y}{b} = \frac{x}{{x - a}},\] где координаты \(x\) и \(y\) удовлетворяют соотношениям \(x > a,\) \(y > b.\) Отсюда выразим \(y\) через \(x:\) \[y = \frac{{bx}}{{x - a}}.\] Площадь треугольника будет описываться следующей функцией \(S\left( x \right):\) \[ {S\left( x \right) = \frac{{xy}}{2} = \frac{x}{2} \cdot \frac{{bx}}{{x - a}} } = {\frac{{b{x^2}}}{{2\left( {x - a} \right)}}.} \] Вычислим производную: \[ {S'\left( x \right) = {\left( {\frac{{b{x^2}}}{{2\left( {x - a} \right)}}} \right)^\prime } } = {\frac{b}{2}{\left( {\frac{{{x^2}}}{{x - a}}} \right)^\prime } } = {\frac{b}{2} \cdot \frac{{2x\left( {x - a} \right) - {x^2}}}{{{{\left( {x - a} \right)}^2}}} } = {\frac{b}{2} \cdot \frac{{2{x^2} - 2ax - {x^2}}}{{{{\left( {x - a} \right)}^2}}} } = {\frac{{bx\left( {x - 2a} \right)}}{{{{\left( {x - a} \right)}^2}}}.} \] Функция \(S\left( x \right)\) имеет критические точки \(x = 0,\) \(x = a,\) \(x = 2.\) Поскольку \(x > a,\) то решением является точка \(x = 2a.\) При переходе через нее производная меняет знак с минуса на плюс, т.е. \(x = 2a\) − точка минимума функции \(S\left( x \right).\)
Вычислим другой катет треугольника: \[\require{cancel} y = \frac{{bx}}{{x - a}} = \frac{{b \cdot 2a}}{{2a - a}} = \frac{{2\cancel{a}b}}{\cancel{a}} = 2b. \] Таким образом, треугольник с наименьшей площадью имеет катеты, равные \(2a\) и \(2b.\)
|
|
Пример 2
|
|
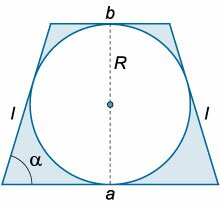
Равнобедренная трапеция описана вокруг окружности радиуса \(R\) (рисунок \(2\)). При каком угле при основании \(\alpha\) площадь заштрихованной области будет наименьшей?
Решение.
Площадь равнобедренной трапеции определяется формулой \[{S_T} = \frac{{a + b}}{2} \cdot h,\] где \(a, b\) − основания трапеции, \(h\) − ее высота. Очевидно, что \(h = 2R.\) Площадь круга равна \({S_K} = \pi {R^2}.\) Тогда площадь заштрихованной области составляет \[ {S = {S_T} - {S_K} = \frac{{a + b}}{2} \cdot 2R - \pi {R^2} } = {\left( {a + b} \right)R - \pi {R^2}.} \] Поскольку трапеция описана вокруг окружности, то сумма противоположных сторон у нее одинакова, т.е. \[ {a + b = 2\ell\;\;\text{или}\;\;} {a + b = 2 \cdot \frac{{2R}}{{\sin \alpha }} } = {\frac{{4R}}{{\sin \alpha }}.} \] Здесь через \(\ell\) обозначена боковая сторона трапеции. Подставляя \(\left( {a + b} \right)\) в предыдущее соотношение, получаем: \[ {S = S\left( \alpha \right) = \frac{{4R}}{{\sin \alpha }} \cdot R - \pi {R^2} } = {{R^2}\left( {\frac{4}{{\sin \alpha }} - \pi } \right).} \] Исследуем площадь \(S\left( \alpha \right)\) на экстремальное значение. Вычислим производную \(S'\left( \alpha \right):\) \[ {S'\left( \alpha \right) = {\left[ {{R^2}\left( {\frac{4}{{\sin \alpha }} - \pi } \right)} \right]^\prime } } = {4{R^2}\left( { - \frac{1}{{{{\sin }^2}\alpha }}} \right) \cdot \cos \alpha } = { - \frac{{4{R^2}\cos \alpha }}{{{{\sin }^2}\alpha }}.} \] Видно, что производная равна нулю при условии \[\cos \alpha = 0,\;\; \Rightarrow \alpha = \frac{\pi }{2},\] причем при переходе через эту точку (при возрастании \(\alpha\)) производная меняет знак с минуса на плюс. Следовательно, \(\alpha = \large\frac{\pi }{2}\normalsize\) − точка минимума функции \(S\left( \alpha \right).\) В этом случае трапеция "вырождается" в квадрат. Минимальное значение площади фигуры определяется формулой \[{S_{\min }} = {R^2}\left( {4 - \pi } \right).\]
|
|
Пример 3
|
|
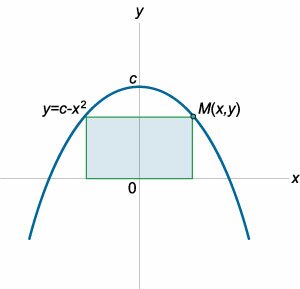
Окно имеет форму прямоугольника, ограниченного сверху полукругом (рисунок \(3\)). Периметр окна равен \(P.\) Определить радиус полукруга \(R,\) при котором площадь окна является наибольшей.
Решение.
Очевидно, что одна сторона прямоугольника равна \(2R.\) Другую сторону обозначим через \(y.\) Периметр всего окна выражается формулой \[P = \pi R + 2R + 2y.\] Отсюда находим \(y:\) \[y = \frac{1}{2}\left[ {P - \left( {\pi + 2} \right)R} \right].\] Площадь окна составляет: \[ {S = \frac{{\pi {R^2}}}{2} + 2Ry } = {\frac{{\pi {R^2}}}{2} + 2R \cdot \frac{1}{2}\left[ {P - \left( {\pi + 2} \right)R} \right] } = {\frac{{\pi {R^2}}}{2} + PR - \pi {R^2} - 2{R^2} } = {PR - \frac{{\pi {R^2}}}{2} - 2{R^2}.} \] Полученное выражение представляет собой функцию \(S\left( R \right).\) Исследуем ее на экстремум. Находим производную: \[ {S'\left( R \right) = {\left( {PR - \frac{{\pi {R^2}}}{2} - 2{R^2}} \right)^\prime } } = {P - \pi R - 4R } = {P - \left( {\pi + 4} \right)R.} \] Определяем стационарные точки: \[ {S'\left( R \right) = 0,}\;\; {\Rightarrow P - \left( {\pi + 4} \right)R = 0,}\;\; {\Rightarrow R = \frac{P}{{\pi + 4}}.} \] Поскольку вторая производная отрицательна: \[ {S''\left( R \right) = {\left[ {P - \left( {\pi + 4} \right)R} \right]^\prime } } = { - \left( {\pi + 4} \right) < 0,} \] то найденная точка является точкой максимума, т.е. при этом значении \(R\) площадь окна будет наибольшей.
Само максимальное значение площади составляет \[ {{S_{\max }} = PR - \frac{{\pi {R^2}}}{2} - 2{R^2} } = {P\left( {\frac{P}{{\pi + 4}}} \right) - \left( {\frac{\pi }{2} + 2} \right){\left( {\frac{P}{{\pi + 4}}} \right)^2} } = {\frac{{{P^2}}}{{\pi + 4}} - \frac{{\left( {\cancel{\pi + 4}} \right){P^2}}}{{2{{\left( {\pi + 4} \right)}^{\cancel{2}}}}} } = {\frac{{2{P^2} - {P^2}}}{{2\left( {\pi + 4} \right)}} } = {\frac{{{P^2}}}{{2\left( {\pi + 4} \right)}}.} \]
|
|
Пример 4
|
|
В область, ограниченную параболой \(y = c - {x^2}\) и осью \(Ox,\) вписан прямоугольник, стороны которого параллельны координатным осям и одна сторона лежит на оси \(Ox.\) Определить наибольшую площадь прямоугольника.
Решение.
Пусть \(M\left( {x,y} \right)\) − вершина прямоугольника, принадлежащая параболе (рисунок \(4\)). Длины сторон такого прямоугольника равны \(2x\) и \(y.\) Его площадь составляет \[ {S\left( x \right) = 2xy } = {2x\left( {c - {x^2}} \right) } = {2cx - 2{x^3}.} \] Исследуем функцию \(S\left( x \right)\) на экстремум. Производная записывается в виде \[S'\left( x \right) = {\left( {2cx - 2{x^3}} \right)^\prime } = 2c - 6{x^2}.\] Приравнивая производную нулю, находим стационарные точки: \[ {S'\left( x \right) = 0,}\;\; {\Rightarrow 2c - 6{x^2} = 0,}\;\; {\Rightarrow {x^2} = \frac{c}{3},}\;\; {\Rightarrow x = \pm \sqrt {\frac{c}{3}}.} \] Очевидно, что оба корня соответствуют одному и тому же прямоугольнику. Убедимся, что точка \(\sqrt {\large\frac{c}{3}\normalsize} \) является точкой максимума функции \(S\left( x \right).\) Проверим это с помощью второй производной: \[S''\left( x \right) = {\left( {2c - 6{x^2}} \right)^\prime } = - 12x < 0.\] Поскольку \(S''\left( x \right) < 0,\) то \(\sqrt {\large\frac{c}{3}\normalsize} \) является точкой максимума.
Вычислим наибольшую площадь вписанного прямоугольника: \[ {{S_{\max }} = 2\sqrt {\frac{c}{3}} \left[ {c - {{\left( {\sqrt {\frac{c}{3}} } \right)}^2}} \right] } = {2\sqrt {\frac{c}{3}} \cdot \frac{{2c}}{3} } = {4\sqrt {{{\left( {\frac{c}{3}} \right)}^3}}.} \]
|
|
Пример 5
|
|
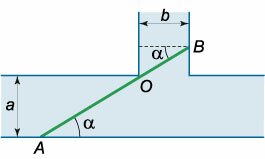
Два канала шириной \(a\) и \(b\) соединяются друг с другом под прямым углом (рисунок \(5\)). Определить наибольшую длину бревен, которые можно сплавлять по данной системе каналов.
Решение.
Пусть положение бревна описывается углом \(\alpha,\) как показано на рисунке \(5.\) Максимально возможная длина бревна \(L\) зависит от угла \(\alpha:\) \[ {L = \left| {AO} \right| + \left| {OB} \right| } = {\frac{a}{{\sin \alpha }} + \frac{a}{{\cos\alpha }} } = {L\left( \alpha \right).} \] Отметим два предельных положения: \[ {\alpha \to 0,}\;\; {\Rightarrow \sin \alpha \to 0,}\;\; {\Rightarrow \left| {AO} \right| \to \infty ;} \] \[ {\alpha \to \frac{\pi }{2},}\;\; {\Rightarrow \cos \alpha \to 0,}\;\; {\Rightarrow \left| {OB} \right| \to \infty .} \] Таким образом, угол \(\alpha\) изменяется в интервале \(0 < \alpha < \large\frac{\pi }{2}\normalsize.\)
Находим производную функции \(L\left( \alpha \right):\) \[ {L'\left( \alpha \right) = \left( { - \frac{a}{{{{\sin }^2}\alpha }}} \right) \cdot \cos \alpha - \frac{b}{{{{\cos }^2}\alpha }} \cdot \left( { - \sin \alpha } \right) } = {\frac{{b\sin \alpha }}{{{{\cos }^2}\alpha }} - \frac{{a\cos \alpha }}{{{\sin^2}\alpha }} } = {\frac{{b\,{{\sin }^3}\alpha - a\,{{\cos }^3}\alpha }}{{{{\cos }^2}\alpha \,{{\sin }^2}\alpha }} } = {\frac{{4\left( {b\,{{\sin }^3}\alpha - a\,{{\cos }^3}\alpha } \right)}}{{{{\sin }^2}\left( {2\alpha } \right)}}.} \] Приравнивая ее нулю, получаем следующее решение: \[ {L'\left( \alpha \right) = 0,}\;\; {\Rightarrow \frac{{4\left( {b\,{{\sin }^3}\alpha - a\,{{\cos }^3}\alpha } \right)}}{{{{\sin }^2}\left( {2\alpha } \right)}} = 0,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {b\,{{\sin }^3}\alpha - a\,{{\cos }^3}\alpha = 0}\\ {{{\sin }^2}\left( {2\alpha } \right) \ne 0} \end{array}} \right.,}\;\; {\Rightarrow b\,{\tan ^3}\alpha - a = 0,}\;\; {\Rightarrow \tan \alpha = \sqrt[\large 3\normalsize]{{\frac{a}{b}}}.} \] Можно убедиться, что при переходе через данное критическое значение \(\alpha\) производная меняет знак с минуса на плюс, т.е. найденная точка является точкой минимума функции \(L\left( \alpha \right).\) (Ясно, что длина бревна должна быть меньше указанного значения, чтобы осуществить поворот из одного канала в другой.)
Выразим синус и косинус угла \(\alpha\) через его тангенс: \[ {1 + {\cot^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }},}\;\; {\Rightarrow \sin \alpha = \frac{1}{{\sqrt {1 + {{\cot }^2}\alpha } }} } = {\frac{1}{{\sqrt {1 + \frac{1}{{{{\tan }^2}\alpha }}} }} } = {\frac{{\tan \alpha }}{{\sqrt {1 + {{\tan }^2}\alpha } }};} \] \[ {1 + {\tan ^2}\alpha = \frac{1}{{{\cos^2}\alpha }},}\;\; {\Rightarrow \cos \alpha = \frac{1}{{\sqrt {1 + {{\tan }^2}\alpha } }}.} \] Теперь можно записать окончательное выражение для максимально возможной длины бревна: \[ {{L_{\max }} = \frac{a}{{\sin \alpha }} + \frac{b}{{\cos\alpha }} } = {\frac{a}{{\frac{{\tan \alpha }}{{\sqrt {1 + {{\tan }^2}\alpha } }}}} + \frac{b}{{\frac{1}{{\sqrt {1 + {{\tan }^2}\alpha } }}}} } = {\sqrt {1 + {{\tan }^2}\alpha } \left( {\frac{a}{{\tan \alpha }} + b} \right) } = {\sqrt {1 + \sqrt[\large 3\normalsize]{{{{\left( {\frac{a}{b}} \right)}^2}}}} \left( {\frac{a}{{\sqrt[\large 3\normalsize]{{\frac{a}{b}}}}} + b} \right) } = {\sqrt {1 + \frac{{{a^{\large\frac{2}{3}\normalsize}}}}{{{b^{\large\frac{2}{3}\normalsize}}}}} \left( {{b^{\large\frac{1}{3}\normalsize}}{a^{\large\frac{1}{3}\normalsize}} + b} \right) } = {\frac{{\sqrt {{a^{\large\frac{2}{3}\normalsize}} + {b^{\large\frac{2}{3}\normalsize}}} }}{{{b^{\large\frac{1}{3}\normalsize}}}} \cdot {b^{\large\frac{1}{3}\normalsize}}\left( {{a^{\large\frac{2}{3}\normalsize}} + {b^{\large\frac{2}{3}\normalsize}}} \right) } = {{\left( {{a^{\large\frac{2}{3}\normalsize}} + {b^{\large\frac{2}{3}\normalsize}}} \right)^{\large\frac{3}{2}\normalsize}}.} \] В частном случае, при равной ширине каналов (когда \(a = b\)), получаем: \[ {{L_{\max }} = \sqrt {{{\left( {2{a^{\large\frac{2}{3}\normalsize}}} \right)}^3}} } = {\sqrt {8{a^2}} = a\sqrt 8 .} \]
|
|
Пример 6
|
|
В эллипс, заданный уравнением \[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,\] вписан прямоугольник со сторонами, параллельными координатным осям (рисунок \(6\)). Найти стороны прямоугольника с наибольшей площадью.
Решение.
Пусть точка \(M\left( {x,y} \right)\) − вершина вписанного прямоугольника. Его площадь равна \[S = 2x \cdot 2y = 4xy.\] Величину \(y\) можно выразить из уравнения эллипса: \[ {\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,}\;\; {\Rightarrow \frac{{{y^2}}}{{{b^2}}} = 1 - \frac{{{x^2}}}{{{a^2}}},}\;\; {\Rightarrow {y^2} = \frac{{{b^2}}}{{{a^2}}}\left( {{a^2} - {x^2}} \right),}\;\; {\Rightarrow y = \pm \frac{b}{a}\sqrt {{a^2} - {x^2}} .} \] В контексте данной задачи мы рассматриваем лишь положительные значения \(x\) и \(y.\) Следовательно, \[ {S = 4xy } = {\frac{{4bx}}{a}\sqrt {{a^2} - {x^2}} } = {S\left( x \right).} \] Для нахождения экстремума функции \(S\left( x \right)\) вычислим производную: \[ {S'\left( x \right) = {\left( {\frac{{4bx}}{a}\sqrt {{a^2} - {x^2}} } \right)^\prime } } = {\frac{{4b}}{a}\left[ {\sqrt {{a^2} - {x^2}} + x \cdot \frac{1}{{2\sqrt {{a^2} - {x^2}} }} \cdot \left( { - 2x} \right)} \right] } = {\frac{{4b}}{a}\left[ {\sqrt {{a^2} - {x^2}} - \frac{{{x^2}}}{{\sqrt {{a^2} - {x^2}} }}} \right] } = {\frac{{4b}}{a} \cdot \frac{{{a^2} - {x^2} - {x^2}}}{{\sqrt {{a^2} - {x^2}} }} } = {\frac{{4b\left( {{a^2} - 2{x^2}} \right)}}{{a\sqrt {{a^2} - {x^2}} }}.} \] Производная равна нулю при условии \[ {{a^2} - 2{x^2} = 0,}\;\; {\Rightarrow {x^2} = \frac{{{a^2}}}{2},}\;\; {\Rightarrow x = \frac{a}{{\sqrt 2 }}.} \] При переходе через точку \(x = \large\frac{a}{{\sqrt 2 }}\normalsize\) производная меняет знак с плюса на минус. Поэтому найденная точка является точкой максимума.
Величина \(y,\) соответственно, равна \[ {y = \frac{b}{a}\sqrt {{a^2} - {x^2}} } = {\frac{b}{a}\sqrt {{a^2} - {{\left( {\frac{a}{{\sqrt 2 }}} \right)}^2}} } = {\frac{b}{a}\sqrt {{a^2} - \frac{{{a^2}}}{2}} } = {\frac{b}{a}\sqrt {\frac{{{a^2}}}{2}} } = {\frac{b}{a} \cdot \frac{a}{{\sqrt 2 }} } = {\frac{b}{{\sqrt 2 }}.} \] Итак, прямоугольник, вписанный в эллипс, будет иметь наибольшую площадь, когда его стороны равны \[ {2x = 2 \cdot \frac{a}{{\sqrt 2 }} = a\sqrt 2 \;\;\;\text{и}\;\;\;} {2y = 2 \cdot \frac{b}{{\sqrt 2 }} = b\sqrt 2 .} \] Максимальная площадь прямоугольника составляет \[{S_{\max }} = a\sqrt 2 \cdot b\sqrt 2 = 2ab.\] Интересно отметить частный случай, когда эллипс имеет равные полуоси, т.е. вырождается в окружность: \[a = b = R.\] В этом случае прямоугольник с наибольшей площадью представляет собой квадрат со стороной \(R\sqrt 2 .\)
|
|
Пример 7
|
|
Картина высотой \(a\) подвешена на стене таким образом, что ее нижний край выше уровня глаз наблюдателя на \(h\) единиц. На каком расстоянии \(x\) от стены должен находиться наблюдатель, чтобы угол обзора картины был наибольшим (рисунок \(7a\))?
Решение.
Выведем соотношение для угла обзора \(\varphi = \angle BPA.\) Из рисунка \(7b\) следует, что \(\varphi = \alpha - \beta ,\) где \[ {\tan \beta = \frac{h}{x},}\;\;\; {\tan \alpha = \frac{{a + h}}{x}.} \] Используя соотношение для тангенса разности, получаем: \[ {\tan \varphi = \tan \left( {\alpha - \beta } \right) } = {\frac{{\tan \alpha - \tan \beta }}{{1 + \tan \alpha \tan \beta }} } = {\frac{{\frac{{a + h}}{x} - \frac{h}{x}}}{{1 + \frac{{a + h}}{x} \cdot \frac{h}{x}}} } = {\frac{{\frac{{a + \cancel{h} - \cancel{h}}}{x}}}{{\frac{{{x^2} + \left( {a + h} \right)h}}{{{x^2}}}}} } = {\frac{{ax}}{{{x^2} + ah + {h^2}}}.} \] Отсюда находим выражение для функции \(\varphi \left( x \right):\) \[ {\varphi = \varphi \left( x \right) } = {\arctan \frac{{ax}}{{{x^2} + ah + {h^2}}}.} \] Вычисляем производную: \[ {\varphi '\left( x \right) = {\left( {\arctan \frac{{ax}}{{{x^2} + ah + {h^2}}}} \right)^\prime } } = {\frac{1}{{1 + {{\left( {\frac{{ax}}{{{x^2} + ah + {h^2}}}} \right)}^2}}} \cdot {\left( {\frac{{ax}}{{{x^2} + ah + {h^2}}}} \right)^\prime } } = {\frac{{{{\left( {{x^2} + ah + {h^2}} \right)}^2}}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {{\left( {ax} \right)}^2}}} } {\cdot \frac{{a\left( {{x^2} + ah + {h^2}} \right) - ax \cdot 2x}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {{\left( {ax} \right)}^2}}} } = {\frac{{a{x^2} + {a^2}h + a{h^2} - 2a{x^2}}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {a^2}{x^2}}} } = {\frac{{{a^2}h + a{h^2} - a{x^2}}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {a^2}{x^2}}} } = {\frac{{a\left( {ah + {h^2} - {x^2}} \right)}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {a^2}{x^2}}}.} \] Производная равна нулю при условии \[ {\varphi '\left( x \right) = 0,}\;\; {\Rightarrow \frac{{a\left( {ah + {h^2} - {x^2}} \right)}}{{{{\left( {{x^2} + ah + {h^2}} \right)}^2} + {a^2}{x^2}}} = 0,}\;\; {\Rightarrow ah + {h^2} - {x^2} = 0,}\;\; {\Rightarrow {x^2} = ah + {h^2},}\;\; {\Rightarrow x = \sqrt {h\left( {a + h} \right)} .} \] причем в этой точке функция \(\varphi \left( x \right)\) имеет максимум, так как знак производной изменяется с плюса на минус при переходе через данное значение.
Таким образом, оптимальное расстояние от стены для наилучшего обзора картины определяется формулой \[x = \sqrt {h\left( {a + h} \right)} .\] Например, если \(a = 3\,\text{м}\) и \(h = 2\,\text{м},\) то оптимальное расстояние составляет \[ {x = \sqrt {h\left( {a + h} \right)} = \sqrt {2\left( {3 + 2} \right)} } = {\sqrt {10} \approx 3,16\,\text{м}.} \]
|
|
Пример 8
|
|
Две стороны параллелограмма лежат на сторонах заданного треугольника, а одна из его вершин принадлежит третьей стороне (рисунок \(8\)). Найти условия, при которых площадь параллелограмма является наибольшей.
Решение.
Пусть треугольник определяется двумя сторонами \(a = BC,\) \(b = AC\) и углом \(\alpha = \angle BCA\) между ними. Построим параллелограмм \(CMKN\) в соответствии с условиями задачи. Обозначим стороны параллелограмма \(x = MK\) и \(y = KN.\) Площадь данного параллелограмма определяется формулой \[S - xy\sin \alpha .\] Выразим \(y\) через \(x\) и стороны треугольника \(a, b.\) Из подобия треугольников \(BMK\) и \(BCA\) следует, что \[\frac{{a - y}}{a} = \frac{x}{b}.\] Тогда \[ {\left( {a - y} \right)b = ax,}\;\; {\Rightarrow ab - by = ax,}\;\; {\Rightarrow by = ab - ax,}\;\; {\Rightarrow y = \frac{{ab - ax}}{b} = a - \frac{a}{b}x.} \] В результате площадь \(S\) записывается как функция \(S\left( x \right):\) \[ {S = S\left( x \right) } = {x\left( {a - \frac{a}{b}x} \right)\sin \alpha } = {ax\sin \alpha - \frac{a}{b}{x^2}\sin \alpha.} \] Находим производную: \[ {S'\left( x \right) = {\left( {ax\sin \alpha - \frac{a}{b}{x^2}\sin \alpha } \right)^\prime } } = {a\sin \alpha - \frac{{2ax}}{b}\sin \alpha } = {a\sin \alpha \left( {1 - \frac{{2x}}{b}} \right).} \] Отсюда видно, что экстремум функции \(S\left( x \right)\) существует в следующей точке: \[ {S'\left( x \right) = 0,}\;\; {\Rightarrow 1 - \frac{{2x}}{b} = 0,}\;\; {\Rightarrow 2x = b,}\;\; {\Rightarrow x = \frac{b}{2}.} \] При переходе через эту точку производная меняет свой знак с плюса на минус, т.е. эта точка является точкой максимума. Другая сторона параллелограмма при этом равна \[ {y = a - \frac{a}{b}x = a - \frac{a}{b} \cdot \frac{b}{2} } ={ a - \frac{a}{2} = \frac{a}{2}.} \] Итак, вписанный в треугольник параллелограмм со сторонами \(x, y\) имеет наибольшую площадь при условии \[x = \frac{b}{2},\;\;y = \frac{a}{2},\] где \(a, b\) − стороны треугольника. Интересно, что результат не зависит от угла \(\alpha\) между сторонами треугольника.
|
|
Пример 9
|
|
Найти цилиндр с наименьшей площадью поверхности.
Решение.
Оптимальная форма цилиндра при заданном объеме позволяет уменьшить расходы на материалы. Поэтому такая задача актуальна, например, при строительстве нефтехранилищ (рисунок \(9\)).
Пусть \(H\) − высота цилиндра, а \(R\) − радиус его основания. Объем и полная площадь поверхности цилиндра вычисляются по формулам \[V = \pi {R^2}H,\;\;\;S = 2\pi {R^2} + 2\pi RH.\] В качестве независимой переменной выберем радиус основания \(R.\) Выразим \(H\) через \(R\) (при заданном объеме \(V\)): \[H = \frac{V}{{\pi {R^2}}}.\] Исследуем площадь поверхности \(S\left( R \right)\) на экстремум. \[ {S\left( R \right) = 2\pi {R^2} + 2\pi RH } = {2\pi {R^2} + 2\pi R \cdot \frac{V}{{\pi {R^2}}} } = {2\pi {R^2} + \frac{{2V}}{R}.} \] Вычисляем производную: \[ {S'\left( R \right) = {\left( {2\pi {R^2} + \frac{{2V}}{R}} \right)^\prime } } = {4\pi R - \frac{{2V}}{{{R^2}}} } = {\frac{{4\pi {R^3} - 2V}}{{{R^2}}}.} \] Находим стационарные точки: \[ {S'\left( R \right) = 0,}\;\; {\Rightarrow \frac{{4\pi {R^3} - 2V}}{{{R^2}}} = 0,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {4\pi {R^3} - 2V = 0}\\ {{R^2} \ne 0} \end{array},} \right.}\;\; {\Rightarrow R = \sqrt[\large 3\normalsize]{{\frac{V}{{2\pi }}}}.} \] Данное значение \(R\) соответствует минимальной площади поверхности \(S\left( R \right),\) поскольку при переходе через эту точку производная меняет знак с минуса на плюс.
Вычислим теперь высоту найденного цилиндра: \[ {H = \frac{V}{{\pi {R^2}}} } = {\frac{V}{{\pi {{\left( {\sqrt[\large 3\normalsize]{{\frac{V}{{2\pi }}}}} \right)}^2}}} } = {\frac{{{2^{\large\frac{2}{3}\normalsize}}{\pi ^{\large\frac{2}{3}\normalsize}}V}}{{\pi {V^{\large\frac{2}{3}\normalsize}}}} } = {\frac{{{2^{\large\frac{2}{3}\normalsize}}{V^{\large\frac{1}{3}\normalsize}}}}{{{\pi ^{\large\frac{1}{3}\normalsize}}}} } = {\sqrt[\large 3\normalsize]{{\frac{{4V}}{\pi }}}.} \] Отношение высоты к радиусу основания составляет \[ {\frac{H}{R} = \frac{{\sqrt[\large 3\normalsize]{{\frac{{4V}}{\pi }}}}}{{\sqrt[\large 3\normalsize]{{\frac{V}{{2\pi }}}}}} } = {\sqrt[\large 3\normalsize]{{\frac{{4V}}{\pi } \cdot \frac{{2\pi }}{V}}} } = {\sqrt[\large 3\normalsize]{8} = 2.} \] Другими словами, высота цилиндра с наименьшей площадью поверхности должна быть равна его диаметру, т.е. осевое сечение такого цилиндра представляет собой квадрат.
|
|
Пример 10
|
|
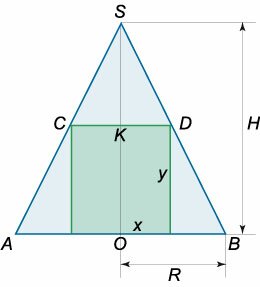
Определить наибольший объем цилиндра, вписанного в конус с радиусом основания \(R\) и высотой \(H\) (рисунок \(10a\)).
Решение.
Обозначим радиус основания вписанного цилиндра через \(x,\) а его высоту − через \(y\) (рисунок \(10b\)). Из подобия треугольников \(SKD\) и \(SOB\) следует, что \[ {\frac{{KD}}{{OB}} = \frac{{SK}}{{SO}}}\;\;\; {\text{или}\;\;\;\frac{x}{R} = \frac{{H - y}}{H}.} \] Записанное уравнение устанавливает связь между переменными \(x\) и \(y.\) Выразим \(y\) через \(x:\) \[ {\frac{x}{R} = \frac{{H - y}}{H},}\;\; {\Rightarrow HX = \left( {H - y} \right)R,}\;\; {\Rightarrow Hx = HR - Ry,}\;\; {\Rightarrow y = \frac{{HR - Hx}}{R} = H\left( {1 - \frac{x}{R}} \right).} \] Объем вписанного цилиндра выражается формулой \[V = \pi {x^2}y.\] Тогда \[ {V\left( x \right) = \pi {x^2}H\left( {1 - \frac{x}{R}} \right) } = {\pi H\left( {{x^2} - \frac{{{x^3}}}{R}} \right).} \] Найдем наибольшее значение функции \(V\left( x \right):\) \[ {V'\left( x \right) = {\left[ {\pi H\left( {{x^2} - \frac{{{x^3}}}{R}} \right)} \right]^\prime } } = {\pi H\left( {2x - \frac{{3{x^2}}}{R}} \right);} \] \[ {V'\left( x \right) = 0,}\;\; {\Rightarrow \pi H\left( {2x - \frac{{3{x^2}}}{R}} \right) = 0,}\;\; {\Rightarrow 2x - \frac{{3{x^2}}}{R} = 0,}\;\; {\Rightarrow x\left( {2 - \frac{{3x}}{R}} \right) = 0,}\;\; {\Rightarrow {x_1} = 0,\;{x_2} = \frac{{2R}}{3}.} \] Решение \({x_1} = 0\) соответствует цилиндру с нулевым объемом и не имеет физического смысла. При переходе через точку \({x_2} = \large\frac{{2R}}{3}\normalsize\) производная меняет знак с плюса на минус. Поэтому, \(x = \large\frac{{2R}}{3}\normalsize\) является точкой максимума функции \(V\left( x \right).\) Для данного основания высота цилиндра будет составлять \[ {y = H\left( {1 - \frac{x}{R}} \right) } = {H\left( {1 - \frac{{2\cancel{R}}}{{3\cancel{R}}}} \right) = \frac{H}{3}.} \] Следовательно, наибольший объем вписанного в конус цилиндра равен \[ {{V_{\max }} = \pi {x^2}y } = {\pi {\left( {\frac{{2R}}{3}} \right)^2} \cdot \frac{H}{3} } = {\frac{4}{{27}}\pi {R^2}H.} \] Это составляет \(\large\frac{4}{9}\normalsize\) от объема конуса.
|
|
Пример 11
|
|
Найти конус наибольшего объема, вписанный в шар радиуса \(R.\)
Решение.
Рассмотрим осевое сечение вписанного в шар конуса (рисунок \(11\)). Введем следующие обозначения: \(H\) − высота конуса, \(r\) − радиус основания конуса, \(\alpha\) − угол между радиусом и основанием конуса. Радиус основания и высота конуса связаны с радиусом шара следующими соотношениями: \[r = R\cos \alpha ,\;\;\;H = R\sin \alpha + R.\] В таком случае объем конуса можно представить в виде \[ {V = \frac{1}{3}\pi {r^2}H } = {\frac{1}{3}\pi {\left( {R\cos \alpha } \right)^2}\left( {R\sin \alpha + R} \right) } = {\frac{1}{3}\pi {R^3}{\cos ^2}\alpha \left( {\sin \alpha + 1} \right).} \] где угол \(\alpha\) изменяется в интервале \(0 < \alpha < \large\frac{\pi }{2}\normalsize.\) Дифференцируем объем \(V\) по переменной \(\alpha:\) \[ {V'\left( \alpha \right) } = {{\left[ {\frac{1}{3}\pi {R^3}{{\cos }^2}\alpha \left( {\sin \alpha + 1} \right)} \right]^\prime } } = {\frac{1}{3}\pi {R^3}{\left[ {{{\cos }^2}\alpha \left( {\sin \alpha + 1} \right)} \right]^\prime } } = {\frac{1}{3}\pi {R^3}\left[ {2\cos \alpha \cdot \left( { - \sin \alpha } \right) \cdot \left( {\sin \alpha + 1} \right) + {{\cos }^2}\alpha \cdot \cos \alpha } \right] } = {\frac{1}{3}\pi {R^3}\cos \alpha \left[ {{{\cos }^2}\alpha - 2{{\sin }^2}\alpha - 2\sin \alpha } \right];} \] \[ {V'\left( \alpha \right) = 0,}\;\; {\Rightarrow \frac{1}{3}\pi {R^3}\cos \alpha \left[ {{{\cos }^2}\alpha - 2{{\sin }^2}\alpha - 2\sin \alpha } \right] = 0.} \]
-
\(\cos \alpha = 0,\;\; \Rightarrow \alpha = \large\frac{\pi }{2}\normalsize;\)
-
\( {{\cos ^2}\alpha - 2{\sin ^2}\alpha - 2\sin \alpha = 0,}\;\; {\Rightarrow 1 - 3{\sin ^2}\alpha - 2\sin \alpha = 0,}\;\; {\Rightarrow 3{\sin ^2}\alpha + 2\sin \alpha - 1 = 0,}\;\; {\Rightarrow \sin \alpha = t,}\;\; {\Rightarrow 3{t^2} + 2t - 1 = 0,}\;\; {\Rightarrow D = 4 - 4 \cdot 3 \cdot \left( { - 1} \right) = 16,}\;\; {\Rightarrow {t_{1,2}} = \frac{{ - 2 \pm \sqrt {16} }}{6};}\;\; \) \[{t_1} = - 1,\;\; \Rightarrow \sin\alpha = - 1,\;\; \Rightarrow \;\;\alpha = \frac{{3\pi }}{2},\] \[{t_2} = \frac{1}{3},\;\; \Rightarrow \sin \alpha = \frac{1}{3}.\]
Как видно, решением является \(\sin \alpha = \large\frac{1}{3}\normalsize.\) Можно убедиться, что при возрастании угла \(\alpha\) и переходе через данную точку производная меняет свой знак с плюса на минус, т.е. здесь достигается максимальное значение объема конуса.
Вычислим косинус угла \(\alpha:\) \[ {\cos\alpha = \sqrt {1 - {{\left( {\frac{1}{3}} \right)}^2}} } = {\sqrt {1 - \frac{1}{9}} = \frac{{2\sqrt 2 }}{3}.} \] Тогда радиус основания и высота конуса наибольшего объема имеют такие значения: \[r = \frac{{2\sqrt 2 }}{3}R,\;\;\;H = R \cdot \frac{1}{3} + R = \frac{4}{3}R.\] Объем такого конуса равен \[ {V = \frac{1}{3}\pi {r^2}H } = {\frac{\pi }{3} \cdot {\left( {\frac{{2\sqrt 2 }}{3}} \right)^2} \cdot \frac{4}{3}R } = {\frac{\pi }{3} \cdot \frac{8}{9}{R^2} \cdot \frac{4}{3}R } = {\frac{{32}}{{81}}\pi {R^3}.} \] что составляет \(\large\frac{{8}}{{27}}\normalsize\) от объема шара.
|
|
Пример 12
|
|
Тело имеет форму цилиндра, основания которого завершаются полусферами (рисунок \(12\)). Определить высоту цилиндра \(H\) и радиус полусфер \(R,\) при которых площадь поверхности при заданном объеме \(V\) будет наименьшей.
Решение.
Объем тела выражается формулой \[ {V = \frac{4}{3}\pi {R^3} + \pi {R^2}H } = {\pi {R^2}\left( {\frac{{4R}}{3} + H} \right).} \] Выразим отсюда высоту \(H:\) \[H = \frac{V}{{\pi {R^3}}} - \frac{{4R}}{3}.\] Рассмотрим площадь полной поверхности тела: \[S = 4\pi {R^2} + 2\pi RH.\] Подставим в эту формулу выражение для \(H:\) \[ {S = S\left( R \right) } = {4\pi {R^2} + 2\pi R\left( {\frac{V}{{\pi {R^3}}} - \frac{{4R}}{3}} \right) } = {4\pi {R^2} + \frac{{2V}}{R} - \frac{{8\pi {R^2}}}{3} } = {\frac{{4\pi {R^2}}}{3} + \frac{{2V}}{R}.} \] Вычислим производную функции \(S\left( R \right):\) \[ {S'\left( R \right) } = {{\left( {\frac{{4\pi {R^2}}}{3} + \frac{{2V}}{R}} \right)^\prime } } = {\frac{{4\pi }}{3} \cdot 2R - \frac{{2V}}{{{R^2}}} } = {\frac{{8\pi R}}{3} - \frac{{2V}}{{{R^2}}} } = {\frac{{8\pi {R^3} - 6V}}{{3{R^2}}}.} \] Приравнивая производную нулю, получаем: \[ {S'\left( R \right) = 0,}\;\; {\Rightarrow \frac{{8\pi {R^3} - 6V}}{{3{R^2}}} = 0,}\;\; {\Rightarrow {R^3} = \frac{{3V}}{{4\pi }},}\;\; {\Rightarrow R = \sqrt[\large 3\normalsize]{{\frac{{3V}}{{4\pi }}}}.} \] Найденная точка, очевидно, является точкой минимума функции \(S\left( R \right),\) поскольку при переходе через нее производная меняет свой знак с минуса на плюс. Вычислим соответствующее значение высоты цилиндра: \[ {H = \frac{V}{{\pi {R^3}}} - \frac{{4R}}{3} } = {\frac{V}{{\pi {{\left( {\sqrt[\large 3\normalsize]{{\frac{{3V}}{{4\pi }}}}} \right)}^3}}} - \frac{4}{3}\sqrt[\large 3\normalsize]{{\frac{{3V}}{{4\pi }}}} } = {\frac{{V \cdot {4^{\large\frac{2}{3}\normalsize}} \cdot {\pi ^{\large\frac{2}{3}\normalsize}}}}{{\pi \cdot {3^{\large\frac{2}{3}\normalsize}} \cdot {V^{\large\frac{2}{3}\normalsize}}}} - \frac{{4 \cdot {3^{\large\frac{1}{3}\normalsize}} \cdot {V^{\large\frac{1}{3}\normalsize}}}}{{3 \cdot {4^{\large\frac{1}{3}\normalsize}} \cdot {\pi ^{\large\frac{1}{3}\normalsize}}}} } = {\frac{{{V^{\large\frac{1}{3}\normalsize}} \cdot {4^{\large\frac{2}{3}\normalsize}}}}{{{\pi ^{\large\frac{1}{3}\normalsize}} \cdot {3^{\large\frac{2}{3}\normalsize}}}} - \frac{{{V^{\large\frac{1}{3}\normalsize}} \cdot {4^{\large\frac{2}{3}\normalsize}}}}{{{\pi ^{\large\frac{1}{3}\normalsize}} \cdot {3^{\large\frac{2}{3}\normalsize}}}} \equiv 0.} \] Как видно, наиболее оптимальной является просто шаровая поверхность без цилиндрической части!
|
|
Пример 13
|
|
В шар радиусом \(a\) вписан цилиндр. Найти радиус основания \(R\) и высоту \(H\) цилиндра, имеющего наибольший объем.
Решение.
Объем цилиндра равен \[V = \pi {R^2}H.\] Радиус основания цилиндра \(R\) связан с радиусом шара \(a\) следующим соотношением (рисунок \(13\)): \[ {{a^2} = {R^2} + {\left( {\frac{H}{2}} \right)^2} } = {{R^2} + \frac{{{H^2}}}{4}.} \] Следовательно, \[{R^2} = {a^2} - \frac{{{H^2}}}{4}.\] Подставляя это в формулу для объема цилиндра, получаем: \[ {V = \pi {R^2}H = \pi \left( {{a^2} - \frac{{{H^2}}}{4}} \right)H } = {\pi {a^2}H - \frac{{\pi {H^3}}}{4}.} \] Данное выражение представляет собой функцию \(V\left( H \right),\) которое мы будем исследовать далее на экстремум. Производная \(V'\left( H \right)\) имеет вид: \[ {V'\left( H \right) = {\left( {\pi {a^2}H - \frac{{\pi {H^3}}}{4}} \right)^\prime } } = {\pi {a^2} - \frac{{3\pi {H^2}}}{4} } = {\frac{\pi }{4}\left( {4{a^2} - 3{H^2}} \right).} \] Корни производной равны: \[ {V'\left( H \right) = 0,}\;\; {\Rightarrow 4{a^2} - 3{H^2} = 0,}\;\; {\Rightarrow {H^2} = \frac{{4{a^2}}}{3},}\;\; {\Rightarrow H = \pm \frac{{2a}}{{\sqrt 3 }}.} \] Разумеется, нас устраивает лишь положительное значение \(H = \large\frac{{2a}}{{\sqrt 3 }}\normalsize.\) При переходе через эту точку производная меняет знак с плюса на минус, т.е. здесь существует максимум функции \(V\left( H \right).\) При такой высоте \(H\) радиус основания цилиндра равен \[ {{R^2} = {a^2} - \frac{{{H^2}}}{4} } = {{a^2} - \frac{1}{4}{\left( {\frac{{2a}}{{\sqrt 3 }}} \right)^2} } = {{a^2} - \frac{{4{a^2}}}{{12}} } = {{a^2} - \frac{{{a^2}}}{3} } = {\frac{{2{a^2}}}{3},}\;\; {\Rightarrow R = a\sqrt {\frac{2}{3}} .} \] Итак, вписанный в шар цилиндр имеет наибольший объем при условии \[H = \frac{{2a}}{{\sqrt 3 }},\;\;\;R = a\sqrt {\frac{2}{3}} ,\] где \(a\) − радиус шара. Максимальное значение объема составляет \[ {V = \pi {R^2}H } = {\pi {\left( {a\sqrt {\frac{2}{3}} } \right)^2} \cdot \frac{{2a}}{{\sqrt 3 }} } = {\frac{{2\pi {a^2}}}{3} \cdot \frac{{2a}}{{\sqrt 3 }} } = {\frac{{4\pi {a^3}}}{{3\sqrt 3 }},} \] т.е. меньше объема шара в \(\sqrt 3\) раз.
|
|
Пример 14
|
|
Бревно длиной \(H\) имеет форму усеченного конуса c радиусами оснований \(R\) и \(r\) (\(R > r\)). Из данного бревна требуется вырезать балку в форме параллелепипеда с квадратным сечением наибольшего объема.
Решение.
Будем считать, что оси бревна и балки совпадают. Усеченный конус и вписанный в него параллелепипед схематически показаны в разрезе на рисунке \(14.\) Объем параллелепипеда определяется формулой \[V = {x^2}y,\] где \(x\) − сторона квадрата в основании параллелепипеда, а \(y\) − его высота.
Рассматривая подобные треугольники \(CBR\) и \(CKM,\) можно записать следующую пропорцию: \[ {\frac{{MK}}{{AB}} = \frac{{MC}}{{AC}},}\;\; {\Rightarrow \frac{y}{H} = \frac{{R - \frac{x}{2}}}{{R - r}}.} \] Отсюда находим высоту \(y:\) \[y = \frac{{H\left( {R - \frac{x}{2}} \right)}}{{R - r}}.\] Запишем объем \(V\) как функцию \(x:\) \[ {V = V\left( x \right) } = {{x^2}y = \frac{{{x^2}H\left( {R - \frac{x}{2}} \right)}}{{R - r}} } = {\frac{H}{{R - r}}\left( {R{x^2} - \frac{{{x^3}}}{2}} \right).} \] Производная имеет вид: \[ {V'\left( x \right) } = {{\left[ {\frac{H}{{R - r}}\left( {R{x^2} - \frac{{{x^3}}}{2}} \right)} \right]^\prime } } = {\frac{H}{{R - r}}\left( {2Rx - \frac{{3{x^2}}}{2}} \right) } = {\frac{{Hx}}{{R - r}}\left( {2R - \frac{{3x}}{2}} \right).} \] Находим стационарную точку: \[ {V'\left( x \right) = 0,}\;\; {\Rightarrow \frac{{Hx}}{{R - r}}\left( {2R - \frac{{3x}}{2}} \right) = 0,}\;\; {\Rightarrow 2R - \frac{{3x}}{2} = 0,}\;\; {\Rightarrow x = \frac{{4R}}{3}.} \] Слева от данной точки производная положительна, а справа − отрицательна. Следовательно, найденная точка является точкой максимума функции \(V\left( x \right).\) В таком случае высота параллелепипеда составляет \[ {y = \frac{{H\left( {R - \frac{x}{2}} \right)}}{{R - r}} } = {\frac{{H\left( {R - \frac{{4R}}{6}} \right)}}{{R - r}} } = {\frac{{HR\left( {1 - \frac{2}{3}} \right)}}{{R - r}} } = {\frac{{HR}}{{3\left( {R - r} \right)}}.} \] Итак параллелепипед, вписанный в усеченный конус, имеет наибольший объем, если его стороны равны \[x = \frac{{4R}}{3},\;\;\;y = \frac{{HR}}{{3\left( {R - r} \right)}}.\]
|
|
Пример 15
|
|
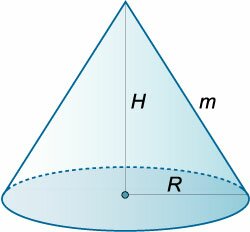
Конус имеет объем \(V.\) При каком радиусе основания \(R\) и высоте \(H\) площадь боковой поверхности конуса является наименьшей?
Решение.
Обозначим образующую конуса через \(m\) (рисунок \(15a\)). Площадь боковой поверхности конуса выражается формулой \[{S_{\text{бок}}} = \pi Rm.\] Далее площадь боковой поверхности будет обозначать просто буквой \(S.\) Учитывая, что объем конуса равен \[V = \frac{1}{3}\pi {R^2}H,\] выразим высоту \(H\) через \(R\) и \(V:\) \[H = \frac{{3V}}{{\pi {R^2}}}.\] По теореме Пифагора находим: \[ {m = \sqrt {{H^2} + {R^2}} } = {\sqrt {{{\left( {\frac{{3V}}{{\pi {R^2}}}} \right)}^2} + {R^2}} .} \] Тогда площадь боковой поверхности записывается как функция радиуса основания \(R:\) \[ {S = \pi Rm } = {\pi R\sqrt {{{\left( {\frac{{3V}}{{\pi {R^2}}}} \right)}^2} + {R^2}} } = {\pi R\sqrt {\frac{{9{V^2}}}{{{\pi ^2}{R^4}}} + {R^2}} } = {\pi R\sqrt {\frac{{9{V^2} + {\pi ^2}{R^6}}}{{{\pi ^2}{R^4}}}} } = {\frac{{\cancel{\pi} \cancel{R}}}{{\cancel{\pi} {R^{\cancel{2}}}}}\sqrt {9{V^2} + {\pi ^2}{R^6}} } = {\frac{{\sqrt {9{V^2} + {\pi ^2}{R^6}} }}{R}.} \] Вычисляем производную: \[ {S'\left( R \right) } = {{\left( {\frac{{\sqrt {9{V^2} + {\pi ^2}{R^6}} }}{R}} \right)^\prime } } = {\frac{{\frac{{6{\pi ^2}{R^5}}}{{2\sqrt {9{V^2} + {\pi ^2}{R^6}} }} \cdot R - \sqrt {9{V^2} + {\pi ^2}{R^6}} \cdot 1}}{{{R^2}}} } = {\frac{{6{\pi ^2}{R^6} - 2\left( {9{V^2} + {\pi ^2}{R^6}} \right)}}{{2{R^2}\sqrt {9{V^2} + {\pi ^2}{R^6}} }} } = {\frac{{4{\pi ^2}{R^6} - 18{V^2}}}{{2{R^2}\sqrt {9{V^2} + {\pi ^2}{R^6}} }} } = {\frac{{2{\pi ^2}{R^6} - 9{V^2}}}{{{R^2}\sqrt {9{V^2} + {\pi ^2}{R^6}} }}.} \] Производная равна нулю при условии \[ 2{\pi ^2}{R^6} - 9{V^2} = 0,\;\; \Rightarrow {R^6} = \frac{{9{V^2}}}{{2{\pi ^2}}},\;\; \Rightarrow R = \sqrt[\large 6\normalsize]{{\frac{{9{V^2}}}{{2{\pi ^2}}}}}. \] Видно, что при увеличении \(R\) и переходе через найденную стационарную точку производная меняет знак с минуса на плюс. Следовательно, здесь функция \(S\left( R \right)\) имеет минимум.
Определим высоту конуса: \[ {H = \frac{{3V}}{{\pi {R^2}}} } = {\frac{{3V}}{{\pi \sqrt[\large 3\normalsize]{{\frac{{9{V^2}}}{{2{\pi ^2}}}}}}} } = {\frac{{3V}}{{\pi \cdot \frac{{{3^{\frac{2}{3}}} \cdot {V^{\frac{2}{3}}}}}{{{2^{\frac{1}{3}}} \cdot {\pi ^{\frac{2}{3}}}}}}} } = {\frac{{{3^{\large\frac{1}{3}\normalsize}} \cdot {V^{\large\frac{1}{3}\normalsize}} \cdot {2^{\large\frac{1}{3}\normalsize}}}}{{{\pi ^{\large\frac{1}{3}\normalsize}}}} } = {\sqrt[\large 3\normalsize]{{\frac{{6V}}{\pi }}}.} \] Чтобы лучше представить форму оптимального конуса, вычислим отношение \(\large\frac{H}{R}\normalsize:\) \[ {\frac{H}{R} = \frac{{\sqrt[\large 3\normalsize]{{\frac{{6V}}{\pi }}}}}{{\sqrt[\large 6\normalsize]{{\frac{{9{V^2}}}{{2{\pi ^2}}}}}}} } = {\frac{{{3^{\large\frac{1}{3}\normalsize}} \cdot {2^{\large\frac{1}{3}\normalsize}} \cdot {V^{\large\frac{1}{3}\normalsize}}}}{{{\pi ^{\large\frac{1}{3}\normalsize}}}}:\frac{{{3^{\large\frac{1}{3}\normalsize}} \cdot {V^{\large\frac{1}{3}\normalsize}}}}{{{2^{\large\frac{1}{6}\normalsize}} \cdot {\pi ^{\large\frac{1}{3}\normalsize}}}} } = {\frac{{\cancel{3^{\large\frac{1}{3}\normalsize}} \cdot {2^{\large\frac{1}{3}\normalsize}} \cdot \cancel{V^{\large\frac{1}{3}\normalsize}} \cdot \cancel{\pi ^{\large\frac{1}{3}\normalsize}} \cdot {2^{\large\frac{1}{6}\normalsize}}}}{{\cancel{\pi ^{\large\frac{1}{3}\normalsize}} \cdot \cancel{3^{\large\frac{1}{3}\normalsize}} \cdot \cancel{V^{\large\frac{1}{3}\normalsize}}}} } = {{2^{\large\frac{1}{2}\normalsize}} = \sqrt 2 .} \] Таким образом, высота конуса с наименьшей площадью боковой поверхности должна быть примерно в \(1,4\) раза больше радиуса основания.
Интересно, каково отношение высоты к радиусу основания такого мегасооружения конусообразной формы как Хан Шатыр (рисунок \(15b\))? Если площадь боковой поверхности являлась одним из критических факторов при проектировании, то, вероятно, его форма должна быть близка к полученному решению.
|
|
|
|