Второй закон Ньютона

Второй закон Ньютона устанавливает связь между силой \(\mathbf{F},\) действующей на тело массы \(m,\) и ускорением \(\mathbf{a},\) которое приобретает тело под действием этой силы.

Ускорение тела  \(\mathbf{a}\) прямо пропорционально действующей силе  \(\mathbf{F}\) и обратно пропорционально массе тела \(m,\) то есть \[\mathbf{a} = \frac{\mathbf{F}}{m}\;\;\text{или}\;\;\mathbf{F} = m\mathbf{a} = m\frac{{{d^2}\mathbf{r}}}{{d{t^2}}}.\] Данная формулировка справедлива для систем с постоянной массой. В случае, когда масса тела изменяется (например, при релятивистском движении), второй закон Ньютона имеет вид \[\mathbf{F} = \frac{{d\mathbf{p}}}{{dt}},\] где \(\mathbf{p}\) − импульс (количество движения) тела.
В общем случае сила \(\mathbf{F}\) зависит от координат тела, т.е. радиус-вектора \(\mathbf{r},\) его скорости \(\mathbf{v}\) и времени \(t:\) \[\mathbf{F} = \mathbf{F}\left( {\mathbf{r},\mathbf{v},t} \right).\] Ниже мы рассмотрим частные случаи, когда сила \(\mathbf{F}\) зависит лишь от одной из указанных переменных. В предположении, что движение одномерное, второй закон Ньютона в этом случае записывается в виде дифференциального уравнения второго порядка: \[m\frac{{{d^2}x}}{{d{t^2}}} = F\left( t \right).\] Интегрируя один раз, находим закон изменения скорости тела \(v\left( t \right):\) \[v\left( t \right) = {v_0} + \frac{1}{m}\int\limits_0^t {F\left( \tau \right)d\tau } .\] Здесь мы считаем, что тело начинает двигаться в момент \(t = 0\) с начальной скоростью \(v\left( {t = 0} \right) = {v_0}.\) Интегрируя еще раз, получаем закон движения \(x\left( t \right):\) \[x\left( t \right) = {x_0} + \int\limits_0^t {v\left( \tau \right)d\tau } ,\] где \({x_0}\) − начальная координата тела, \(\tau\) − переменная интегрирования. При движении твердого тела в жидкой или газообразной среде на него действует сила сопротивления (или вязкого трения). При малых скоростях \(\mathbf{v}\) эта сила пропорциональна скорости \(\mathbf{v}:\) \[\mathbf{F} = - k\mathbf{v}.\] Коэффициент \(k,\) в свою очередь, пропорционален вязкости среды \(\eta.\) В частности, если тело имеет шарообразную форму, то сила сопротивления описывается законом Стокса: \[\mathbf{F} = - 6\pi \eta R\mathbf{v},\] где \(R\) − радиус шара, \(\eta\) − вязкость среды.

При таком режиме движения второй закон Ньютона записывается (в одномерном приближении) в виде следующего дифференциального уравнения: \[m\frac{{{d^2}x}}{{d{t^2}}} = m\frac{{dv}}{{dt}} = - kv.\] Интегрируя это уравнение при начальном условии \(v\left( {t = 0} \right) = {v_0},\) получаем \[ {\frac{{dv}}{v} = - \frac{k}{m}dt,}\;\; {\Rightarrow \int\limits_{{v_0}}^v {\frac{{du}}{u}} = - \frac{k}{m}\int\limits_0^t {d\tau } .} \] Здесь \(u\) и \(\tau\) − переменные интегрирования. Скорость тела изменяется от \({v_0}\) до \(v\) за время от \(0\) до \(t.\) Следовательно, \[ {\ln v - \ln {v_0} = - \frac{k}{m}t,}\;\; {\Rightarrow \ln \frac{v}{{{v_0}}} = - \frac{k}{m}t,}\;\; {\Rightarrow v\left( t \right) = {v_0}{e^{ - {\large\frac{k}{m}\normalsize}t}}.} \] Таким образом, если сила сопротивления среды пропорциональна скорости тела, то его скорость будет уменьшаться по экспоненциальному закону.

Закон движения \(x\left( t \right)\) легко определяется повторным интегрированием: \[ {x\left( t \right) = {x_0} + \int\limits_0^t {v\left( \tau \right)d\tau } } = {{x_0} + \int\limits_0^t {{v_0}{e^{ - {\large\frac{k}{m}\normalsize}\tau }}d\tau } } = {{x_0} - \frac{{m{v_0}}}{k}\left( {{e^{ - {\large\frac{k}{m}\normalsize}t}} - 1} \right) } = {{x_0} + \frac{{m{v_0}}}{k}\left( {1 - {e^{ - {\large\frac{k}{m}\normalsize} t}}} \right).} \] Из последней формулы видно, что путь пройденный телом до полной остановки, будет равен \(\large\frac{{m{v_0}}}{k}\normalsize,\) т.е. пропорционален начальному импульсу тела \(m{v_0}.\)

При увеличении скорости движения тела физика процесса изменяется. Кинетическая энергия тела начинает расходоваться не только на трение между слоями жидкости, но и на перемещение объема жидкости впереди тела. В этом режиме сила сопротивления становится пропорциональной квадрату скорости: \[F = - \mu \rho S{v^2},\] где \(\mu\) − коэффициент пропорциональности, \(S\) − площадь поперечного сечения тела, \(\rho\) − плотность среды.

Описанный нелинейный режим возникает при условии \[\mathbf{\text{Re}} = \frac{{\rho vL}}{\eta } > 100,\] где \(\mathbf{\text{Re}}\) − безразмерное число Рейнольдса, \(\eta\) − вязкость среды, \(L\) − характерный поперечный размер, например, радиус тела.

Рассматривая одномерное движение, запишем второй закон Ньютона для этого случая в виде \[m\frac{{{d^2}x}}{{d{t^2}}} = m\frac{{dv}}{{dt}} = - \mu \rho S{v^2}.\] Интегрируя, находим закон изменения скорости: \[ {\frac{{dv}}{{{v^2}}} = - \frac{{\mu \rho S}}{m}dt,}\;\; {\Rightarrow \int\limits_{{v_0}}^v {\frac{{du}}{{{u^2}}}} = - \frac{{\mu \rho S}}{m}\int\limits_0^t {d\tau } .} \] Здесь \(u\) и \(\tau\) снова обозначают переменные интегрирования. За время \(t\) скорость тела будет уменьшаться от начального значения \({v_0}\) до конечного значения \(v.\) В результате получаем \[ {- \left( {\frac{1}{v} - \frac{1}{{{v_0}}}} \right) = - \frac{{\mu \rho S}}{m}t,}\;\; {\Rightarrow \frac{1}{v} = \frac{1}{{{v_0}}} + \frac{{\mu \rho S}}{m}t,}\;\; {\Rightarrow v\left( t \right) = \frac{1}{{\frac{1}{{{v_0}}} + \frac{{\mu \rho S}}{m}t}} = \frac{{{v_0}}}{{1 + \frac{{\mu \rho S{v_0}}}{m}t}}.} \] Интегрируем еще раз, чтобы найти закон движения \(x\left( t \right):\) \[\require{cancel} {x\left( t \right) = \int\limits_0^t {\frac{{{v_0}}}{{1 + \frac{{\mu \rho S{v_0}}}{m}\tau }}d\tau } } = {\int\limits_0^t {\frac{{\cancel{v_0}}}{{1 + \frac{{\mu \rho S{v_0}}}{m}\tau }}\frac{{d\left( {1 + \frac{{\mu \rho S{v_0}}}{m}\tau } \right)}}{{\frac{{\mu \rho S\cancel{v_0}}}{m}}}} } = {\frac{m}{{\mu \rho S}}\int\limits_0^t {\frac{{d\left( {1 + \frac{{\mu \rho S{v_0}}}{m}\tau } \right)}}{{1 + \frac{{\mu \rho S{v_0}}}{m}\tau }}} } = {\frac{m}{{\mu \rho S}}\left[ {\left. {\ln \left( {1 + \frac{{\mu \rho S{v_0}}}{m}\tau } \right)} \right|_0^t} \right] } = {\frac{m}{{\mu \rho S}}\ln \left( {1 + \frac{{\mu \rho S{v_0}}}{m}t} \right).} \] Необходимо учитывать, что полученные формулы справедливы при достаточно больших значениях скорости: при снижении скорости данная модель становится физически некорректной, поскольку сила сопротивления начинает линейно зависеть от скорости (Этот случай был рассмотрен нами ранее). Примерами сил, зависящих лишь от координаты, является, в частности:

• Сила упругости \(F = -kx;\)

• Сила гравитационного притяжения \(F = - G\large\frac{{{m_1}{m_2}}}{{{x^2}}}\normalsize.\)

Движение тела массой \(m\) (груза на пружинке) под действием силы упругости будет определяться дифференциальным уравнением \[m\frac{{{d^2}x}}{{d{t^2}}} = - kx\;\;\text{или}\;\;\frac{{{d^2}x}}{{d{t^2}}} + \frac{k}{m}x = 0.\] Это уравнение описывает незатухающие периодические колебания с периодом \[T = 2\pi \sqrt {\frac{m}{k}} .\] В случае гравитационного притяжения движение тела описывается нелинейным дифференциальным уравнением \[\frac{{{d^2}x}}{{d{t^2}}} = - G\frac{M}{{{x^2}}},\] где \(M\) − масса притягивающего тела (например, масса Земли или Солнца), \(G\) − универсальная гравитационная постоянная.

Решение этого уравнения приводится на странице Закон всемирного тяготения.

В случае, когда сила зависит от координаты, ускорение удобно представить в таком виде: \[a = \frac{{dv}}{{dt}} = \frac{{dv}}{{dx}}\frac{{dx}}{{dt}} = v\frac{{dv}}{{dx}}.\] Тогда дифференциальное уравнение можно записать как \[m\frac{{{d^2}x}}{{d{t^2}}} = m\frac{{dv}}{{dt}} = mv\frac{{dv}}{{dx}} = F\left( x \right).\] Разделяя переменные \(v\) и \(x,\) получаем \[ {mvdv = F\left( x \right)dx,}\;\; {\Rightarrow m\int\limits_{{v_0}}^v {udu} = \int\limits_0^L {F\left( x \right)dx} ,}\;\; {\Rightarrow \frac{{m{v^2}}}{2} - \frac{{mv_0^2}}{2} = \int\limits_0^L {F\left( x \right)dx} .} \] Последнее равенство выражает закон сохранения энергии. Левая часть описывает изменение кинетической энергии, а правая часть − работу переменной силы \({F\left( x \right)}\) при перемещении тела на расстояние \(L.\)

Последующее интегрирование функции \({v\left( t \right)}\) позволяет найти закон движения тела \({x\left( t \right)}.\) К сожалению, это не всегда можно сделать аналитически из-за громоздкости выражения для \({v\left( t \right)}.\)

   Пример 1

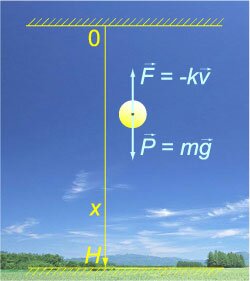
Тело начинает падать с высоты \(H\) под действием силы тяжести. В процессе падения оно испытывает сопротивление, пропорциональное скорости. Определить время падения. На тело действуют две силы (рисунок \(1\)): сила тяжести \(P = mg\) и сила сопротивления \(F = -kv.\) Направим ось \(Ox\) вертикально вниз. Будем считать, что начальная координата равна \(x = 0\) и в момент падения она составляет \(x = H.\) В проекции на ось \(Ox\) уравнение динамики записывается в виде: \[m\frac{{{d^2}x}}{{d{t^2}}} = mg - k\frac{{dx}}{{dt}}.\] Задача представляет собой вариацию случая \(2,\) когда сила зависит от скорости.

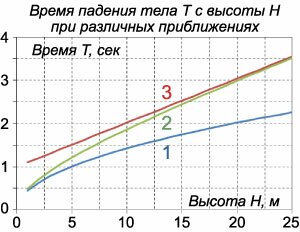
Сначала определим закон изменения скорости \({v\left( t \right)}\) из уравнения \[m\frac{{dv}}{{dt}} = mg - kv,\;\; \Rightarrow \frac{{dv}}{{dt}} = g - \frac{k}{m}v.\] Разделяя переменные, получаем \[\frac{{dv}}{{g - \frac{k}{m}v}} = dt,\;\; \Rightarrow \int\limits_0^v {\frac{{du}}{{g - \frac{k}{m}u}}} = t.\] Здесь \(v\) означает скорость в момент \(t,\) \(u\) − переменная интегрирования. Решение имеет следующий вид: \[ {- \frac{m}{k}\int\limits_0^v {\frac{{d\left( {g - \frac{k}{m}u} \right)}}{{g - \frac{k}{m}u}}} = t,}\;\; {\Rightarrow - \frac{m}{k}\left. {\left[ {\ln \left( {g - \frac{k}{m}u} \right)} \right]} \right|_0^v = t,}\;\; {\Rightarrow \ln \frac{{g - \frac{k}{m}u}}{g} = - \frac{k}{m}t,}\;\; {\Rightarrow \ln \left( {1 - \frac{k}{{mg}}v} \right) = - \frac{k}{m}t,}\;\; {\Rightarrow 1 - \frac{k}{{mg}}v = {e^{ - {\large\frac{k}{m}\normalsize} t}},}\;\; {\Rightarrow \frac{k}{{mg}}v = 1 - {e^{ - {\large\frac{k}{m}\normalsize} t}},}\;\; {\Rightarrow v\left( t \right) = \frac{{mg}}{k}\left( {1 - {e^{ - {\large\frac{k}{m}\normalsize} t}}} \right).} \] Интегрируем еще раз: \[ {x\left( t \right) = \frac{{mg}}{k}\int\limits_0^t {\left( {1 - {e^{ - {\large\frac{k}{m}\normalsize} \tau }}} \right)d\tau } } = {\frac{{mg}}{k}\left[ {\left( {t + \frac{m}{k}{e^{ - {\large\frac{k}{m}\normalsize} t}}} \right) - \left( {0 + \frac{m}{k}{e^{ - {\large\frac{k}{m}\normalsize}0}}} \right)} \right] } = {\frac{{mg}}{k}\left[ {t - \frac{m}{k}\left( {1 - {e^{ - {\large\frac{k}{m}\normalsize} t}}} \right)} \right].} \] Допустим, что тело в момент \(t = T\) достигает поверхности Земли, т.е. проходит путь \(x = H.\) Как видно, время \(T\) определяется неявным алгебраическим уравнением \[H = \frac{{mg}}{k}\left[ {T - \frac{m}{k}\left( {1 - {e^{ - {\large\frac{k}{m}\normalsize}T}}} \right)} \right].\] Значение \(T\) можно оценить приближенно, учитывая, что член \({{e^{ - {\large\frac{k}{m}\normalsize} T}}}\) стремится к нулю при больших \(T.\) Тогда \[ {H \approx \frac{{mg}}{k}\left( {T - \frac{m}{k}} \right)}\;\; {\text{или}\;\;T\left( H \right) \approx \frac{{kH}}{{mg}} + \frac{m}{k}.} \] Полученная приближенная зависимость \(T\left( H \right)\) является линейной, то есть соответствует равномерному движению тела. Ее график (при \(m = 1\;\text{кг},\) \(k = 1\;\text{Н} \cdot \large\frac{\text{с}}{\text{м}}\normalsize\)) показан выше на рисунке \(2\) (красная прямая \(3\)). На этом же рисунке для сравнения показаны два других графика \(T\left( H \right),\) описывающих:

• падение тела в поле тяжести без учета сопротивления воздуха (синяя кривая \(1\)). В этом случае зависимость \(T\left( H \right)\) определяется формулой \(T = \sqrt {\large\frac{{2H}}{g}\normalsize} ;\)

• точное решение нелинейного алгебраического уравнения для \(T\) (зеленая кривая \(2\)).

Из этих графиков видно, что сила сопротивления воздуха практически компенсирует силу тяжести уже через несколько секунд после начала падения. После этого движение тела происходит равномерно. Поэтому при падении с большой высоты (в данном примере это более \(20\;\text{м}\)) для оценки времени падения вполне можно использовать приближенную формулу \(T\left( H \right).\)

   Пример 2

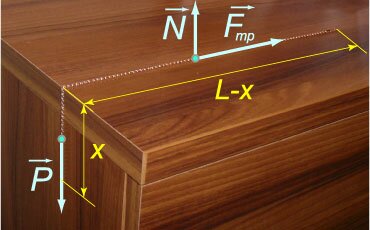
В начальный момент цепочка длиной \(L\) свисает над краем стола таким образом, что сила тяжести уравновешена силой трения (рисунок \(3\)). В результате небольшого смещения \(\varepsilon\) цепочка начинает скользить. Определить время \(T,\) за которое цепочка полностью соскользнет со стола. Коэффициент трения между цепочкой и поверхностью стола равен \(\mu.\) Движение цепочки будет полностью определяться двумя переменными силами:

• силой тяжести \(P = \large\frac{{mgx}}{L}\normalsize,\) где \(x\) − длина части цепочки, свисающей со стола, \(m\) − масса цепочки, \(L\) − ее длина, \(g\) − ускорение свободного падения;

• силой трения \({F_{\text{тр}}} = - \mu mg\large\frac{{L - x}}{L}\normalsize,\) где \(\mu\) − коэффициент трения. Сила трения действует лишь на часть цепочки, лежащую на столе. Длина этой части равна \(L - x.\)

Согласно второму закону Ньютона, дифференциальное уравнение движения цепочки имеет вид: \[ {m\frac{{{d^2}x}}{{d{t^2}}} = P - {F_{\text{тр}}},}\;\; {\Rightarrow m\frac{{{d^2}x}}{{d{t^2}}} = mg\frac{x}{L} - \mu mg\frac{{L - x}}{L},}\;\; {\Rightarrow \frac{{{d^2}x}}{{d{t^2}}} = g\frac{x}{L} - \mu g\frac{{L - x}}{L},}\;\; {\Rightarrow \frac{{{d^2}x}}{{d{t^2}}} - \frac{{\left( {1 + \mu } \right)g}}{L}x = - \mu g.} \] Мы получили неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Найдем решение этого уравнения. Сначала рассмотрим соответствующее однородное уравнение: \[\frac{{{d^2}x}}{{d{t^2}}} - \frac{{\left( {1 + \mu } \right)g}}{L}x = 0.\] Корни характеристического уравнения имеют следующие значения: \[{n^2} - \frac{{\left( {1 + \mu } \right)g}}{L} = 0,\;\; \Rightarrow {n_{1,2}} = \pm \sqrt {\frac{{\left( {1 + \mu } \right)g}}{L}} .\] Тогда общее решение однородного уравнения записывается как \[{x_0} = {C_1}{e^{\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} t}} + {C_2}{e^{ - \sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} t}}.\] Постоянные \({C_1}, {C_2}\) мы определим позже из начальных условий.

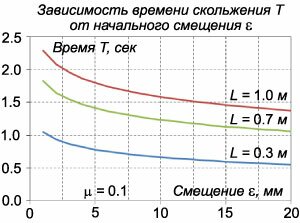
Построим теперь частное решение неоднородного уравнения. В правой части находится постоянное выражение, поэтому будем искать частное решение также в виде постоянного числа: \({x_1} = A.\) Подставляя \({x_1} = A,\) \({x''_1} = 0\) в исходное уравнение, получаем: \[ {0 - \frac{{\left( {1 + \mu } \right)g}}{L}A = - \mu g,}\;\; {\Rightarrow A = \frac{{\mu \cancel{g}L}}{{\left( {1 + \mu } \right)\cancel{g}}} = \frac{{\mu L}}{{1 + \mu }}.} \] Итак, общее решение неоднородного уравнения имеет вид: \[ {x = {x_0} + {x_1} } = {{C_1}{e^{\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} t}} + {C_2}{e^{ - \sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} t}} } + {\frac{{\mu L}}{{1 + \mu }}.} \] Рассмотрим начальные условия и определим коэффициенты \({C_1}\) и \({C_2}.\) Поскольку цепочка находилась в равновесии, то справедливо равенство \[P = {F_{\text{тр}}},\;\; \Rightarrow mg\frac{x}{L} = \mu mg\frac{{L - x}}{L}.\] Отсюда следует, что длина свисающей части цепочки при равновесии составляет \[x = \frac{{\mu L}}{{1 + \mu }}.\] По условию задачи в начальный момент цепочка получает дополнительное смещение \(\varepsilon,\) так что начальные условия записываются в виде: \[\left\{ \begin{array}{l} x\left( {t = 0} \right) = \frac{{\mu L}}{{1 + \mu }} + \varepsilon \\ v\left( {t = 0} \right) = 0 \end{array} \right..\] Теперь можно вычислить коэффициенты \({C_1}\) и \({C_2}:\) \[ {\left\{ \begin{array}{l} {C_1} \cdot 1 + {C_2} \cdot 1 + \cancel{\frac{{\mu L}}{{1 + \mu }}} = \cancel{\frac{{\mu L}}{{1 + \mu }}} + \varepsilon \\ {C_1} \cdot \sqrt {\frac{{\left( {1 + \mu } \right)g}}{L}} - {C_2} \cdot \sqrt {\frac{{\left( {1 + \mu } \right)g}}{L}} = 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {C_1} + {C_2} = \varepsilon \\ {C_1} - {C_2} = 0 \end{array} \right.,}\;\; {\Rightarrow {C_1} = {C_2} = \frac{\varepsilon }{2}.} \] Таким образом, скольжение цепочки описывается законом \[ {x\left( t \right) } = {\frac{\varepsilon }{2}{e^{\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} t}} + \frac{\varepsilon }{2}{e^{ - \sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} t}} } + {\frac{{\mu L}}{{1 + \mu }}.} \] Цепочка полностью соскользнет со стола в момент времени \(T,\) когда \(x\left( T \right) = L.\) В результате для определения \(T\) получаем следующее алгебраическое уравнение: \[ {\frac{\varepsilon }{2}{e^{\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} T}} + \frac{\varepsilon }{2}{e^{ - \sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} T}} } + {\frac{{\mu L}}{{1 + \mu }} = L.} \] Выражение для \(T\) можно записать в явном виде. Для этого умножим уравнение на \({e^{\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} T}}:\) \[\frac{\varepsilon }{2}{e^{2\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} T}} - \frac{L}{{1 + \mu }}{e^{\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} T}} + \frac{\varepsilon }{2} = 0.\] Обозначив \(z = {e^{\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} T}},\) приходим к квадратному уравнению: \[ {\varepsilon {z^2} - \frac{{2L}}{{1 + \mu }}z + \varepsilon = 0,}\;\; {\Rightarrow D = \frac{{4{L^2}}}{{{{\left( {1 + \mu } \right)}^2}}} - 4{\varepsilon ^2},}\;\; {\Rightarrow {z_{1,2}} = \frac{{\frac{{2L}}{{1 + \mu }} \pm \sqrt {\frac{{4{L^2}}}{{{{\left( {1 + \mu } \right)}^2}}} - 4{\varepsilon ^2}} }}{{2\varepsilon }} } = {\frac{L}{{\left( {1 + \mu } \right)\varepsilon }} \pm \sqrt {\frac{{{L^2}}}{{{{\left( {1 + \mu } \right)}^2}{\varepsilon ^2}}} - 1} .} \] Здесь нас устраивает лишь корень со знаком \(+,\) чтобы соблюдалось неравенство \[{e^{\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} T}} > {e^{ - \sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} T}}.\] Следовательно, решение имеет вид \[ {{e^{\sqrt {\large\frac{{\left( {1 + \mu } \right)g}}{L}\normalsize} T}} = \frac{L}{{\left( {1 + \mu } \right)\varepsilon }} + \sqrt {\frac{{{L^2}}}{{{{\left( {1 + \mu } \right)}^2}{\varepsilon ^2}}} - 1} ,}\;\; {\Rightarrow T = \sqrt {\frac{L}{{\left( {1 + \mu } \right)g}}} \ln \left[ {\frac{L}{{\left( {1 + \mu } \right)\varepsilon }} + \sqrt {\frac{{{L^2}}}{{{{\left( {1 + \mu } \right)}^2}{\varepsilon ^2}}} - 1} } \right].} \] Интересно, что в данной модели время соскальзывания \(T\) существенно зависит от величины начального смещения \(\varepsilon\) относительно положения равновесия. При \(\varepsilon \to 0\) формально получаем \(T \to \infty.\) Зависимости времени соскальзывания \(T\) от смещения \(\varepsilon\) для цепочек разной длины \(L\) показаны выше на рисунке \(4.\)